Das Einfärben von Landkarten und die Gröbner-Basen

(Dieses Bild ist Eigentum der Seite mathscareers.org.uk, die freundlicherweise die Erlaubnis erteilte, es in dieser Arbeit benutzen zu dürfen.)

Autor: Marcelo Escudeiro Hernandes

Übersetzt von Herbert Glaser, Kristin Landeck und Hans-Georg Weigand (Universität Würzburg)

Nach dem berühmten „Vier-Farben-Satz“ benötigen wir nur 4 Farben, um eine Landkarte so zu färben, dass benachbarte Gebiete nicht dieselbe Farbe haben. Unter Verwendung von Polynomgleichungen und Gröbner-Basen können wir berechnen, wann drei Farben für das Färben einer ausgewählten Landkarte ausreichen.

1. Das Einfärben von Landkarten
Der berühmte Vier-Farben-Satz (1) besagt, dass alle Landkarten, ob in der Ebene oder auf der Kugel, mit vier verschiedenen Farben so gefärbt werden können, dass benachbarte Gebiete nicht dieselbe Farbe haben. Es ist leicht, Landkarten zu entwerfen, die nicht mit drei Farben ausgemalt werden können, und auch solche, bei denen dies möglich ist. Um zu entscheiden, ob drei Farben zum Färben einer speziellen Landkarte ausreichen, analysiert man ein System von Polynomen, das die Landkarte repräsentiert. Jede Farbe wird durch eine komplexe kubische Einheitswurzel und jedes Gebiet wird durch eine Variable $x_i$ so codiert, dass die Variable nur einen der drei Werte annehmen kann, der für eine der drei Farben steht. Somit erhalten wir die Bedingung ${x_i}^3 - 1 = 0$ für jedes Gebiet.

Für zwei Gebiete, vertreten durch $x_j$ und $x_k$ , gilt die Bedingung $0= x_j ^3 -x_k ^3 =(x_j -x_k)(x_j ^2 +x_j x_k + x_k ^2)$ . Wenn $x_j$ und $x_k$ benachbarte Regionen vertreten, und d benachbarte Regionen nicht die gleiche Farbe haben können, gilt $x_j \neq x_k$ , d.h. $x_j ^2+ x_j x_k + x_k ^2=0$ . Auf diese Weise kann eine Landkarte mit $n$ Gebieten genau dann mit drei Farben gefärbt werden, wenn das System von Polynomgleichungen

(1) $\begin{eqnarray*} \left\{ \begin{array}{l} x_i ^3-1=0 ~,\\ x_j ^2+ x_j x_k + x_k ^2=0 ~, \end{array}\right. \end{eqnarray*}$

für $i= 1 , ... , n$ mindestens eine Lösung besitzt, wobei $x_j$ , $x_k$ angrenzende Gebiete vertreten.

Beispiel 1

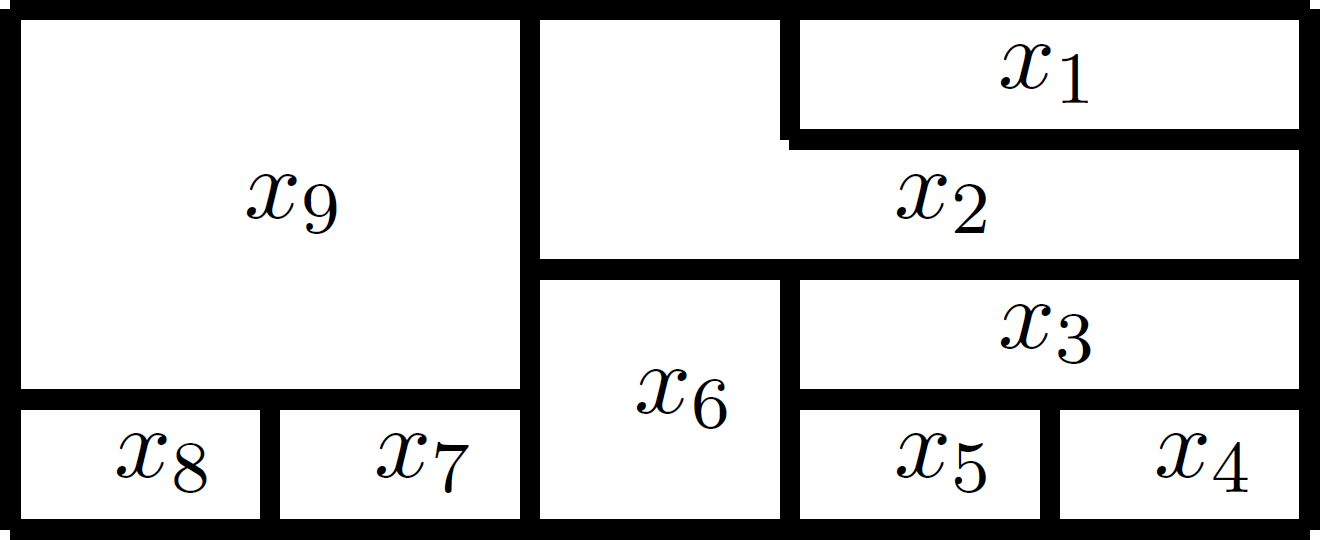
Wir betrachten folgende Landkarte:

Abb.1

Ist es möglich diese Landkarte mit $3$ Farben auszumalen?

Um diese Frage beantworten zu können, müssen wir überprüfen, ob das polynomiale Gleichungssystem (1) mit $i = 1, ..., 9$ und

gelöst werden kann.

2. Systeme von Polynomgleichungen

Viele mathematische Probleme lassen sich mit polynomialen Gleichungssystemen lösen. Wenn die Gleichungen linear sind, können wir sie mit dem Gaußschen Elimininationsverfahren durch ein äquivalentes System ersetzen, dessen Lösung aber einfacher ist. Für nicht lineare Gleichungssysteme beschreiben wir im Folgenden ein analoges Verfahren.

Sei $P(n)$ die Menge der Polynome mit komplexen Koeffizienten in den Variablen $x_1 , ... , x_n$ . Für eine Menge von Polynomen $f_1, ... , f_r$ aus $P(n)$ beschreiben wir das erzeugende Ideal durch

$I = \langle f_1, ... , f_r \rangle = \{ h_1 f_1 + ... + h_r f_r \mid h_1 , ... , h_r \in P(n) \}.$

Ein Satz von David Hilbert <http://www.mat.uniroma1.it/people/manetti/dispense/nullstellen.pdf”>(2), nämlich der Hilbertsche Nullstellensatz besagt, dass das System $f_1 = ... = f_r = 0$ genau dann eine (komplexe) Lösung besitzt, wenn $1 \notin \langle f_1 , ... , f_r \rangle$ gilt. Wie kann diese Bedingung überprüft werden?

Es ist einfach zu zeigen, dass die zwei Gleichungssysteme $f_1 = ... = f_r = 0$ und $g_1 = ... = g_s = 0$ , mit $f_i, g_j \in P (n)$ die gleiche Lösung haben und die Bedingung

(2) $\begin{eqnarray*} \langle f_1 , ... , f_r \rangle = \langle g_1 , ... , g_r \rangle , \end{eqnarray*}$

erfüllen.

Die Strategie, um ein System $f_1 = ... = f_r = 0$ zu lösen, besteht also darin, Polynome $g_1, ... , g_s$ zu finden, die die Bedingung (2) erfüllen, und mit denen wir testen können, ob ein gegebenes $f \in P (n)$ zu dem Ideal $\langle f_1, ... , f_r \rangle$ gehört oder nicht. Natürlich sollen die Lösungen von (2) auch einfacher zu berechnen sein.

Die theoretische Existenz einer solchen Menge $G = \{ g_1 , ... , g_s \}$ wurde während der ersten Hälfte des letzten Jahrhunderts von dem Mathematiker Wolfgang Gröbner nachgewiesen. Einige Jahre später entwickelte sein Student Bruno Buchberger einen Algorithmus zur Berechnung dieser Menge, die Gröbner-Basen genannt werden. Der Buchberger Algorithmus ist eines der wichtigsten Werkzeuge in der Algebra.

Wenn das Ideal die Form $I = \langle f_1 \rangle$ hat, gilt $f \in I$ genau dann, wenn $f = h_1 f_1$ , d.h. $f$ ist durch $f_1$ teilbar. Analog gilt $f \in \langle f_1 , ... , f_r \rangle$ genau dann, wenn gilt $f = h_1 f_1 + ... + h_r f_r$ , Diese Bedingung lässt etwas Ähnliches vermuten, wenn wir $f$ durch $f_1 , ... , f_r$ dividieren. Und in der Tat können wir ein Polynom in mehreren Variablen durch endlich viele Polynome teilen, wenn die Monome in einer besonderen Art und Weise geordnet sind.

3. Gröbner-Basen

Ein Monom $m$ aus $P (n)$ hat die Form $x_1 ^{a_1} ... x_n ^{a_n}$ , wobei $a_1 , ... , a_n$ natürliche Zahlen sind. Das Monom $x_1 ^0 ... x_n ^0$ wird mit $1$ bezeichnet. Den Divisionsalgorithmus können wir anwenden bei den Ordnungen $\preceq$ auf den Monomen aus $P (n)$ , für die $1 \preceq m$ und $m_1 .m \preceq m_2 .m$ gilt, immer dann wenn $m_1 \preceq m_2$ erfüllt ist.

Ein Beispiel ist die lexikographische Ordnung $\preceq_{Lex}$ mit $x_1 ^{a_1} ... x_n ^{a_n} \preceq_{Lex} x_1 ^{b_1} ... x_n ^{b_n}$ , wenn ein $i$ mit $1 \leqslant i \leqslant n$ derauf existiert, dass $a_i < b_i$ und $a_j = b_j$ für alle $j < i$ .

Fixiert man eine Ordnung für die Monome, so wird das größte Monom eines Polynoms $f$ der Leitterm von $f$ genannt und mit $lt (f)$ .

Eine Gröbner-Basis eines Ideals $I = \langle f_1 , ... , f_r\rangle$ , bezüglich einer vorgegebenen monomialen Ordnung, ist nach Definition jede beliebige Menge $G = \{ g_1 , ... , g_s \}$ aus Elementen von $I$ , wobei der Leitterm eines jeden Elementes von $I$ durch den Leitterm eines Elements von $G$ teilbar ist. Man kann zeigen, dass jede Gröbner-Basis $G$ von $I$ die Bedingung (2) erfüllt.

Folglich gilt $1 \in I$ genau dann, wenn eine Gröbner-Basis von $I$ existiert, die eine nicht negative Konstante für alle $m$ aus $P (n)$ enthält, da $1 \preceq m$ gilt.

$G = \{ f_1 \}$ ist z.B. eine Gröbner-Basis von $\langle f_1 \rangle$ in Bezug auf jede monomiale Ordnung. Aber $G = \{ x+y+z-6, x-y+1, x+y-z \}$ ist keine Gröbner-Basis von $I = \langle x+y+z-6, x-y+1, x+y-z \rangle$ bezüglich der lexikographischen Ordnung, da $lt(x+y+z-6-(x-y+1)) = lt(2y+z-7) = 2y$ nicht durch $x$ mit $x = lt(x + y + z - 6) = lt(x - y + 1) = lt(x + y - z)$ teilbar ist.

Um eine Gröbner-Basis eines Ideals bezüglich einer gewählten monomialen Ordnung zu erhalten, kann man Buchbergers Algorithmus (3) anwenden. Die meisten Computer Algebra System bieten entsprechende Algorithmen an.

Beispielsweise ist $G = \{ x+y +z -6, 2y +z -7, 2z -6 \}$ eine Gröbner-Basis des Ideals $I = \langle x+y+z-6, x-y+1, x+y-z \rangle$ bezüglich der lexikographischen Ordnung.

4. Die Lösung des Problems und andere Anwendungen

Das in Beispiel 1 gegebene System hat bestenfalls eine endliche Anzahl an Lösungen (neun Variable, von denen jede einen von drei Werten anzunehmen kann). Das Problem ist, zu entscheiden, ob das System eine Lösung besitzt und wenn ja, diese zu bestimmen.

Wendet man Buchbergers Algorithmus auf das System in Beispiel 1 an, erhält man folgende Gröbner-Basis $G$ bezüglich der lexikographischen Ordnung:

Somit gilt $1 \notin I$ und infolgedessen besitzt das System Lösungen. Die Gleichungen

$\left\{ \begin{array}{l} x_1 ^3 - 1 = 0 ~,\\ x_2 ^2 + x_2 x_1 + x_1 ^2 = 0 ~,\\ x_5 - x_2 = 0 ~,\\ x_7 - x_2 = 0 ~,\\ x_9 -x_3 = 0 ~, \end{array}\right.$

zeigen: Wir können jede beliebige Farbe für $x_1$ , $x_2 \neq x_1$ , $x_2 = x_5 = x_7$ und $x_3 = x_9$ verwenden.

Da die Farben durch die komplexen kubischen Einheitswurzeln codiert sind, besteht unter den Bedingungen $x_4 + x_3 + x_2 = 0$ , $x_6 + x_3 + x_2 = 0$ und $x_8 + x_3 + x_2 = 0$ die einzige Lösung darin, den Variablen Werte (Farben) zuzuweisen, die für $x_2$ , $x_3$ und $x_4$ verschieden sind. Folglich gilt $x_4 = x_6 = x_8$ . Aus $0 = x_3 ^2 + x_3 x_2 -x_2 x_1 -x_1 ^2 = (x_3 + x_2 + x_1 )(x_3 - x_1 )$ folgt weiterhin $x_3 +x_2 +x_1 = 0$ oder $x_3 -x_1 = 0$ . Also können $x_1$ , $x_2$ und $x_3$ verschiedene Farben vertreten, oder es gilt $x_1 = x_3$ . Somit finden wir abgesehen von Permutationen der Farben alle möglichen Lösungen:

Abb. 2

Gröbner-Basen können auch verwendet werden, um mit Idealen umzugehen, um parametrische Gleichungen, die zu impliziten Gleichungen (z.B. für Flächen und Kurven) gehören, in nicht-parametrische Gleichungen umzuwandeln, um das Minimalpolynom algebraischer Zahlen zu berechnen, um Sätze der Euklidischen Geometrie zu beweisen, um Origami-Konstruktionen zu bestätigen und um Sudoku Rätsel zu lösen (siehe (4), (5) und (6)).

Literatur:

(1) http://www.ipv.pt/millenium/Millenium24/12.pdf

(2) http://www.mat.uniroma1.it/people/manetti/dispense/nullstellen.pdf

(3) https://www.risc.jku.at/people/buchberg/papers/1970-00-00-A.english.pdf

(4) Adams, W. and Loustaunau, P., An Introduction to Gröbner Basis, AMS, Providence RI (1994).

(5) Cox, D; Little, J. and O’Shea, D., Ideals, Varieties and Algorithms, 2nd edition, Springer-Verlag, New York, (1996).

(6) Hernandes, M. E., Um Primeiro Contato com Bases de Gröbner, 28°. Colóquio Brasileiro de Matemática, IMPA, Rio de Janeiro, (2011).

Das Einfärben von Landkarten und die Gröbner-Basen

Related

Leave a Reply Cancel reply

Receive notice of every new vignette.

Search

Meta

Das Einfärben von Landkarten und die Gröbner-Basen

Share this:

Related

Leave a Reply Cancel reply

Receive notice of every new vignette.

Search

Meta