
Abb. 1: Illustration einer Calabi-Yau-Mannigfaltigkeit (Wichtig für die Beschreibung von höherdimensionalen Modellen im Rahmen der Stringtheorie).
1. Die Frage nach der nächsten Dimension
Hat unsere Welt tatsächlich mehr als drei Dimensionen? Falls dies der Fall wäre, hätten dann Objekte in höheren Dimensionen eine Beziehung zu der Welt, die uns umgibt? Ist es überhaupt möglich eine Vorstellung von diesen Objekten zu entwickeln oder entziehen sie sich jeglicher Darstellungsform? Fragen wie diese werden von Schülerinnen und Schülern sicherlich gestellt, wenn Sie im Unterricht über Raumdimensionen sprechen. Schüler wollen eine Vorstellung davon bekommen, was man unter einem vier-, fünf- oder sogar
Diese Beispiele zeigen eine typische mathematische Denkweise: Falls es einfacher oder hilfreich ist, ein reales Phänomen in einem höherdimensionalen Raum zu beschreiben, dann können die drei Dimensionen erweitert werden. Das lässt sich unter formalen Gesichtspunkten einfach erläutern. So lassen sich lineare Gleichungen mit drei Unbekannten als Ebenen im Raum, oder analog lineare Gleichungen mit vier Variablen als dreidimensionale Hyperebenen in einem vierdimensionalen Raum interpretieren. Noch allgemeiner lassen sich lineare Gleichungen mit ![]() Unbekannten als
Unbekannten als ![]() -dimensionale Hyperebenen im
-dimensionale Hyperebenen im ![]() -dimensionalen Raum ansehen. Der Vorteil einer derartigen Erweiterung des Dimensionskonzepts liegt in einer einfacheren und einheitlicheren Beschreibung mathematischer Zusammenhänge beim Verwenden von mehr als drei Variablen. Dabei ist es für formale Berechnungen auf algebraischer und numerischer Ebene nicht nötig, anschauliche Vorstellungen in einem solchen höherdimensionalen Kontext aufzubauen. Trotzdem führt dies einerseits zu der Frage, wie die Ergebnisse solcher Überlegungen in die reale Welt übersetzt werden können. Andererseits besteht die Notwendigkeit Objekte höherer Dimensionen in unserem dreidimensionalen Raum zu beschreiben.
-dimensionalen Raum ansehen. Der Vorteil einer derartigen Erweiterung des Dimensionskonzepts liegt in einer einfacheren und einheitlicheren Beschreibung mathematischer Zusammenhänge beim Verwenden von mehr als drei Variablen. Dabei ist es für formale Berechnungen auf algebraischer und numerischer Ebene nicht nötig, anschauliche Vorstellungen in einem solchen höherdimensionalen Kontext aufzubauen. Trotzdem führt dies einerseits zu der Frage, wie die Ergebnisse solcher Überlegungen in die reale Welt übersetzt werden können. Andererseits besteht die Notwendigkeit Objekte höherer Dimensionen in unserem dreidimensionalen Raum zu beschreiben.
Im Folgenden werden Gedankengänge untersucht, die sich mit der Entwicklung von Darstellungen höherdimensionaler Objekte befassen. Dies geschieht durch die exemplarische Betrachtung eines einfachen vierdimensionalen Objekts, des vierdimensionalen Würfels. Dabei wird verdeutlicht, dass der Zugang zu vier- und höherdimensionalen Würfeln auf verschiedenen Wegen möglich ist. Die umfangreiche Nutzung von Analogieargumenten dient hier als zentraler Ausgangspunkt für das Verständnis höherdimensionaler Objekte.
Im Folgenden werden drei verschiedene Zugänge aufgezeigt und analysiert (Eine ausführliche Beschreibung dieser Zugänge findet sich bei Ruppert 2010):
(1) Projektionen von höherdimensionalen Objekten auf (Hyper)Ebenen,
(2) Schnitte von (Hyper)Würfeln mit einer (Hyper)Ebene,
(3) Eine systematische Erweiterung des Koordinatenkonzepts.
2. Projektionen
Zunächst wird die grundlegende Idee der Beschreibung höherdimensionaler Objekte mittels Projektion auf niedrigere Dimensionen verallgemeinert. Besonders die Orthogonalprojektion entlang einer Raumdiagonalen eines ![]() -dimensionalen Hyperwürfels auf den entsprechenden
-dimensionalen Hyperwürfels auf den entsprechenden ![]() -dimensionalen Teilraum ist dabei leicht zu verallgemeinern.
-dimensionalen Teilraum ist dabei leicht zu verallgemeinern.
Beispiel 1: Projektionen von Quadrat und Würfel
Abb. 2.1: Projektion eines Quadrats (Autor: Sebastian Hammer, Universität Würzburg).
Abb. 2.2:Projektion eines Würfels (Autor: Sebastian Hammer, Universität Würzburg).
Für ![]() sind
sind ![]() die Eckpunkte des Quadrates. Die Projektion von Abb. 2.1 wird durch den Schnitt von Geraden
die Eckpunkte des Quadrates. Die Projektion von Abb. 2.1 wird durch den Schnitt von Geraden
![]() , (
, (![]() )
)
mit der Geraden
![]() .
.
dargestellt.
Dies ist eine orthogonale Projektion. Gleichermaßen wird die orthogonale Projektion eines ![]() -dimensionalen Hyperwürfels vollständig durch die Projektion der Koordinaten der Eckpunkte entlang einer Raumdiagonalen in den entsprechenden
-dimensionalen Hyperwürfels vollständig durch die Projektion der Koordinaten der Eckpunkte entlang einer Raumdiagonalen in den entsprechenden ![]() -dimensionalen Teilraum beschrieben. Wir suchen die Schnittpunkte der Geraden:
-dimensionalen Teilraum beschrieben. Wir suchen die Schnittpunkte der Geraden:
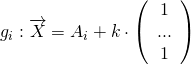 , (
, (![]() )
)
mit der ![]() -Hyperebene
-Hyperebene
![]() .
.
Der Vektor ![]() ist orthogonal zur Hyperebene
ist orthogonal zur Hyperebene ![]() , die Geraden gi sind die orthogonalen Geraden zur Hyperebene
, die Geraden gi sind die orthogonalen Geraden zur Hyperebene ![]() durch die Eckpunkte
durch die Eckpunkte ![]() . Unter Berücksichtigung der Analogie zu den oben beschriebenen Projektionen und der Tatsache, dass z. B. einige Eckpunkte das gleiche Bild unter diesen besonderen Abbildungen haben, erhalten wir Abbildung 3.2 als Darstellung für die entsprechende orthogonale Projektion eines vierdimensionalen Hyperwürfels in den dreidimensionalen Raum.
. Unter Berücksichtigung der Analogie zu den oben beschriebenen Projektionen und der Tatsache, dass z. B. einige Eckpunkte das gleiche Bild unter diesen besonderen Abbildungen haben, erhalten wir Abbildung 3.2 als Darstellung für die entsprechende orthogonale Projektion eines vierdimensionalen Hyperwürfels in den dreidimensionalen Raum.
Eine weitere Möglichkeit, um orthogonale Projektionen vom ![]() -dimensionalen in den
-dimensionalen in den ![]() -dimensionalen Raum (
-dimensionalen Raum (![]() ) zu beschreiben, verwendet die Linearität von orthogonalen Projektionen (als lineare Transformationen). Diese Eigenschaft kann genutzt werden, um zwei-dimensionale Bilder von Würfeln jeder Dimension zu erzeugen und zu verstehen.
) zu beschreiben, verwendet die Linearität von orthogonalen Projektionen (als lineare Transformationen). Diese Eigenschaft kann genutzt werden, um zwei-dimensionale Bilder von Würfeln jeder Dimension zu erzeugen und zu verstehen.
Abbildung 2.2 zeigt drei aufspannende Vektoren des Würfels und deren Bilder unter orthogonaler Projektion entlang der Raumdiagonalen. Alle Eckpunkte des Würfels sind Linearkombinationen dieser Vektoren mit den Koeffizienten ![]() und
und ![]() . Aufgrund der Linearität der Projektion ergeben sich auch die Bilder der Eckpunkte als entsprechende Linearkombinationen der Bilder der aufspannenden Vektoren.
. Aufgrund der Linearität der Projektion ergeben sich auch die Bilder der Eckpunkte als entsprechende Linearkombinationen der Bilder der aufspannenden Vektoren.
Ebenso kann der ![]() -dimensionale Würfel mit adäquaten Linearkombinationen von
-dimensionale Würfel mit adäquaten Linearkombinationen von ![]() linear abhängigen aufspannenden Vektoren beschrieben werden und es gilt: Für den
linear abhängigen aufspannenden Vektoren beschrieben werden und es gilt: Für den ![]() -dimensionalen Würfel gibt es eine orthogonale Projektion in den
-dimensionalen Würfel gibt es eine orthogonale Projektion in den ![]() und eine zugehörige Projektionsebene, so dass die Bilder der aufspannenden Vektoren in die Eckpunkte eines regelmäßigen
und eine zugehörige Projektionsebene, so dass die Bilder der aufspannenden Vektoren in die Eckpunkte eines regelmäßigen ![]() -Ecks zeigen. Gemäß der Additivität ergeben sich daraus durch entsprechende Linearkombinationen schließlich die Bilder aller anderen Eckpunkte. (Für
-Ecks zeigen. Gemäß der Additivität ergeben sich daraus durch entsprechende Linearkombinationen schließlich die Bilder aller anderen Eckpunkte. (Für ![]() betrachte Abbildung 2.2 aus Beispiel 1, mit dem regelmäßigem Dreieck als Bild der aufspannenden Vektoren).
betrachte Abbildung 2.2 aus Beispiel 1, mit dem regelmäßigem Dreieck als Bild der aufspannenden Vektoren).

Abb. 3.1: Projektion eines 4D-Hyperwürfels; acht der projizierten Kanten zeigen auf die Eckpunkte eines 3D Würfels.
Abb. 3.2: Projektion eines 4D-Hyperwürfels.
Beispiel 2: Projektion eines Hyperwürfels
Um zu verstehen, wie die orthogonale Projektion eines ![]() -dimensionalen Hyperwürfels auf einen beliebigen
-dimensionalen Hyperwürfels auf einen beliebigen ![]() -dimensionalen Unterraum erreicht wird, kann man sich zunächst überlegen, wie im dreidimensionalen Raum ein Würfel auf eine Gerade projiziert wird: Für jeden Eckpunkt des Würfels nehme man die orthogonal zur gegebenen Gerade liegende Ebene, welche den Eckpunkt beinhaltet. Der Schnittpunkt der Ebene und der Geraden ist die orthogonale Projektion des Eckpunktes auf die Gerade.
-dimensionalen Unterraum erreicht wird, kann man sich zunächst überlegen, wie im dreidimensionalen Raum ein Würfel auf eine Gerade projiziert wird: Für jeden Eckpunkt des Würfels nehme man die orthogonal zur gegebenen Gerade liegende Ebene, welche den Eckpunkt beinhaltet. Der Schnittpunkt der Ebene und der Geraden ist die orthogonale Projektion des Eckpunktes auf die Gerade.
Analog projiziert man den ![]() -dimensionalen Hyperwürfel auf eine
-dimensionalen Hyperwürfel auf eine ![]() -dimensionale (Hyper)Ebene: Für jeden Eckpunkt des Hyperwürfels nehme man die
-dimensionale (Hyper)Ebene: Für jeden Eckpunkt des Hyperwürfels nehme man die ![]() -dimensionale (Hyper)Ebene, die orthogonal zu der gegebenen
-dimensionale (Hyper)Ebene, die orthogonal zu der gegebenen ![]() -dimensionalen (Hyper)Ebene ist und welche den Eckpunkt enthält. Der Schnittpunkt (!) dieser beiden Hyperebenen ist die orthogonale Projektion des Eckpunktes auf den
-dimensionalen (Hyper)Ebene ist und welche den Eckpunkt enthält. Der Schnittpunkt (!) dieser beiden Hyperebenen ist die orthogonale Projektion des Eckpunktes auf den ![]() -dimensionalen Unterraum.
-dimensionalen Unterraum.
Nun kann eine zweidimensionale Projektion eines fünfdimensionalen Einheitswürfels angegeben werden: Ausgehend von den Bildern der aufspannenden Vektoren (welche in die Eckpunkte eines regelmäßigen Fünfecks zeigen), können durch geeignetes Aneinandersetzen dieser Vektoren die Bilder von sämtlichen Eckpunkten gefunden werden (vgl. Abb. 4.1).
Betrachtet man die Projektion des fünfdimensionalen Würfels, dann spannen die Bilder seiner Kanten die wohlbekannten Penrose-Rauten (vgl. Senechal 1995) auf. Ein weiteres bemerkenswertes Phänomen wird in Abbildung 4.2 aufgezeigt. Unter der Projektion eines sechsdimensionalen Hyperwürfels entlang seiner Raumdiagonalen – die Strecke mit den Endpunkten ![]() bis
bis ![]() – gibt es verschiedene Eckpunkte mit der gleichen Projektion. Die Anzahl der Urbilder wird ebenfalls in Abbildung 4.2 gegeben.
– gibt es verschiedene Eckpunkte mit der gleichen Projektion. Die Anzahl der Urbilder wird ebenfalls in Abbildung 4.2 gegeben.

Abb. 4.1: Projektion eines fünf-dimensionalen Einheitswürfels auf eine geeignete Ebene.
Abb. 4.2: Projektion des sechs-dimensionalen Einheitswürfels auf eine geeignete Ebene.
3. Würfelschnitte
Eine dynamische Möglichkeit zur Darstellung eines vierdimensionalen Hyperwürfels besteht in der Betrachtung von verschiedenen Schnittkörpern, die beim Durchdringen einer drei-dimensionalen Hyperebene entstehen. Zunächst soll ein Würfel (in einem dreidimensionalen Raum) betrachtet werden, der von einer Ebene geschnitten wird. Es wird angenommen, dass sich die Objekte mit (relativer) Geschwindigkeit ![]() bewegen. Besonders einfach lässt sich diese Situation beschreiben, wenn man den Würfel (mit Kantenlänge
bewegen. Besonders einfach lässt sich diese Situation beschreiben, wenn man den Würfel (mit Kantenlänge ![]() ) mit seinen an den Achsen des Koordinatensystems fixierten Kanten betrachtet. Die Ebene
) mit seinen an den Achsen des Koordinatensystems fixierten Kanten betrachtet. Die Ebene
![]()
wandert dann mit der Geschwindigkeit ![]() entlang einer Raumdiagonalen des Würfels durch diesen Würfel hindurch. Da der Würfel selbst ein konvexer Körper ist, genügt es, die Schnittpunkte der Ebene mit den Kanten des Würfels zu jedem Zeitpunkt zu bestimmen. Die Schnittfläche ergibt sich als konvexe Hülle dieser Schnittpunkte. Im Folgenden sind verschiedene Schnittfiguren in chronologischer Reihenfolge dargestellt:
entlang einer Raumdiagonalen des Würfels durch diesen Würfel hindurch. Da der Würfel selbst ein konvexer Körper ist, genügt es, die Schnittpunkte der Ebene mit den Kanten des Würfels zu jedem Zeitpunkt zu bestimmen. Die Schnittfläche ergibt sich als konvexe Hülle dieser Schnittpunkte. Im Folgenden sind verschiedene Schnittfiguren in chronologischer Reihenfolge dargestellt:
In analoger Weise lässt sich nun die Durchdringung eines dreidimensionalen Raumes durch einen vierdimensionalen Hyperwürfel folgendermaßen darstellen: Es wird ein vierdimensionaler Würfel der Kantenlänge a mit einem Raum ![]() geschnitten, der sich mit der Geschwindigkeit
geschnitten, der sich mit der Geschwindigkeit ![]() entlang einer Raumdiagonalen des Hyperwürfels bewegt. Deshalb definieren wir analog:
entlang einer Raumdiagonalen des Hyperwürfels bewegt. Deshalb definieren wir analog:
![]() .
.
Wieder genügt es, die Schnittpunkte des Hyperwürfels mit ![]() zu kennen.
zu kennen.
Eine interaktive Simulation dieser Durchdringung in den Dimensionen eins bis vier wird im folgenden Applet gegeben. (Autor: Rafael Losada, Instituto GeoGebra de Cantabria, Abb. 6).
4. Koordinatengeometrie
Die Einheitsstrecke und das Einheitsquadrat können als ein- bzw. zweidimensionales Analogon des Einheitswürfels angesehen werden. Betrachtet man die Koordinaten der jeweiligen Eckpunkte in einem Koordinatensystem, so ergibt sich:
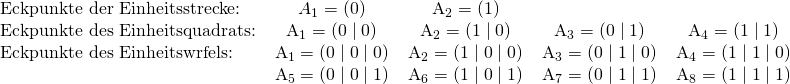
Durch sukzessives Hinzufügen weiterer Koordinaten mit den Koeffizienten ![]() und
und ![]() erhält man die Eckpunktkoordinaten und damit die Anzahl der Eckpunkte eines Einheitshyperwürfels im vier- oder fünfdimensionalen Koordinatensystem. Der Übergang zu Hyperwürfeln in höheren Dimensionen kann also ausschließlich auf der symbolischen Ebene vollzogen und als Fortsetzung des Koordinatenkonzepts verstanden werden. Kombinatorische Überlegungen führen zu folgender Beziehung für die Anzahl
erhält man die Eckpunktkoordinaten und damit die Anzahl der Eckpunkte eines Einheitshyperwürfels im vier- oder fünfdimensionalen Koordinatensystem. Der Übergang zu Hyperwürfeln in höheren Dimensionen kann also ausschließlich auf der symbolischen Ebene vollzogen und als Fortsetzung des Koordinatenkonzepts verstanden werden. Kombinatorische Überlegungen führen zu folgender Beziehung für die Anzahl ![]() der
der ![]() -dimensionalen “Begrenzungswürfel” eines
-dimensionalen “Begrenzungswürfel” eines ![]() -dimensionalen Hyperwürfels (vgl. Graumann, 2009):
-dimensionalen Hyperwürfels (vgl. Graumann, 2009):
![]()
Diese Formel kann durch die folgenden Beobachtungen erhalten werden:
- Jeder
 -dimensionale „Grenzwürfel“ ist parallel zu einer
-dimensionale „Grenzwürfel“ ist parallel zu einer  -dimensionalen Hyperebene, die von
-dimensionalen Hyperebene, die von 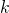 erzeugende Vektoren des
erzeugende Vektoren des 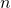 -dimensionalen Würfels aufgespannt wird (vgl. Abschnitt 2).
-dimensionalen Würfels aufgespannt wird (vgl. Abschnitt 2). - 2. Es gibt
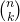 Möglichkeiten
Möglichkeiten 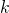 aus
aus 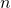 Koeffizienten (bzw. erzeugenden Vektoren) auszuwählen.
Koeffizienten (bzw. erzeugenden Vektoren) auszuwählen. - Es gibt
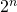 Möglichkeiten einen „Startpunkt“ auszuwählen.
Möglichkeiten einen „Startpunkt“ auszuwählen. - Es gibt
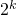 „Startpunkte“ die zum gleichen Grenzwürfel führen.
„Startpunkte“ die zum gleichen Grenzwürfel führen.
Beispiel 3: Der drei-dimensionale Würfel (n=3)
Anzahl der Eckpunkte (![]() ):
): ![]()
Anzahl der Kanten (![]() ):
): ![]()
Anzahl der Oberflächen (![]() ):
): ![]()
Anzahl der Würfel (![]() ):
): ![]()
Dies lässt sich in folgender Tabelle darstellen:
Orientiert man sich zunächst an den gelben Markierungen, so ermöglicht die Tabelle die Interpretation eines einzigen Punktes als einen Würfel der Dimension ![]() , so dass die oben genannte Formel sogar für
, so dass die oben genannte Formel sogar für ![]() gültig ist. Die Anzahl der verschiedenfarbig markierten Folgen legen weitere Vermutungen nahe, die sich mit Hilfe obiger Formel für
gültig ist. Die Anzahl der verschiedenfarbig markierten Folgen legen weitere Vermutungen nahe, die sich mit Hilfe obiger Formel für ![]() beweisen lassen. Beispielsweise:
beweisen lassen. Beispielsweise:
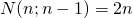 (rote Markierung)
(rote Markierung)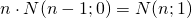 (grüne Markierung)
(grüne Markierung)- Für alle
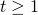 gilt:
gilt: 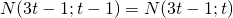 (blaue Markierung)
(blaue Markierung)
Es ergibt sich außerdem eine Rekursionsformel, die es erlaubt, aus den Anzahlen für den ![]() -dimensionalen Würfel die entsprechenden Daten des den
-dimensionalen Würfel die entsprechenden Daten des den ![]() -dimensionalen Würfel zu berechnen.
-dimensionalen Würfel zu berechnen.
Beispiel 4: Beweis der Rekursionsformel
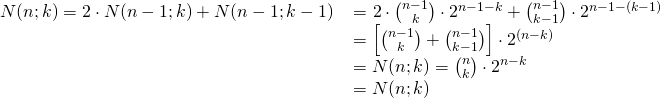
Natürlich können diese algebraischen Darstellungen geometrisch gedeutet und auf die geometrische Situation zurücktransformiert werden.
5. Quasikristalle- Projektionen aus höheren Dimensionen
Gehen wir von der Annahme der klassischen Kristallographie aus, dass das Charakteristikum realer Kristallstrukturen ihre Translationssymmetrie ist (d.h. Invarianz unter drei linear unabhängigen Translationen), so führt dies bei der mathematischen Beschreibung solcher Strukturen auf die “kristallographische Restriktion”, welche nichttriviale Rotationssymmetrien lediglich für die Grade ![]() ,
, ![]() ,
, ![]() und
und ![]() zulässt. Dies entsprach auch den physikalischen Beobachtungen, bis Shechtman et al. (1984) bei einer Al-Mn-Legierung eine aperiodische Kristallstruktur (also eine Struktur ohne Translationssymmetrie) entdeckten, die eine fünfzählige Rotationssymmetrie aufweist. Kristallographen nennen diese Strukturen Quasikristalle. Genauer: Quasikristalle sind strukturelle Formen, die zwar geordnet aber aperiodisch sind. Sie formen Muster, die den gesamten Raum ausfüllen, obwohl ihnen Translationssymmetrien fehlen.
zulässt. Dies entsprach auch den physikalischen Beobachtungen, bis Shechtman et al. (1984) bei einer Al-Mn-Legierung eine aperiodische Kristallstruktur (also eine Struktur ohne Translationssymmetrie) entdeckten, die eine fünfzählige Rotationssymmetrie aufweist. Kristallographen nennen diese Strukturen Quasikristalle. Genauer: Quasikristalle sind strukturelle Formen, die zwar geordnet aber aperiodisch sind. Sie formen Muster, die den gesamten Raum ausfüllen, obwohl ihnen Translationssymmetrien fehlen.
Aber diese Quasikristalle können auch sehr kompliziert sein: Das Fehlen von Translationssymmetrien führt zu einem Mangel an Regeln, die es erlauben zu erklären, wie sich das Muster weiter entfernt von der betrachteten Region entwickelt. Es ist eine Herausforderung dieses Muster zu beschreiben. Ein besonderer Erfolg der Quasikristall-Theorie ist der Nachweis, dass sich viele Quasikristalle als Projektionen eines regelmäßigen Gitters auf einen niedriger dimensionalen affinen Unterraumdarstellen lassen. Betrachten wir ein einfaches Beispiel:
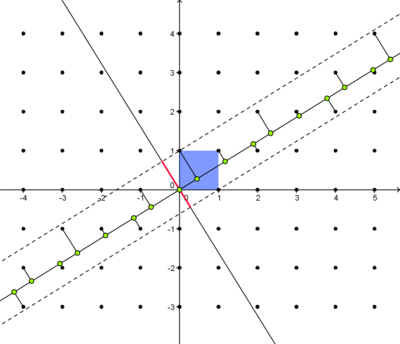
Beispiel 5: Eindimensionaler Quasikristall
Die beiden Geraden ![]() im
im ![]() und
und ![]() im
im ![]() (mit
(mit ![]() ) stehen im Ursprung aufeinander senkrecht. Zunächst betrachtet man die orthogonale Projektion des Einheitsquadrats auf
) stehen im Ursprung aufeinander senkrecht. Zunächst betrachtet man die orthogonale Projektion des Einheitsquadrats auf ![]() (rote Strecke). Nun werden alle Punkte von
(rote Strecke). Nun werden alle Punkte von ![]() , deren Bilder unter der Projektion entlang der Geraden
, deren Bilder unter der Projektion entlang der Geraden ![]() auf der roten Strecke liegen, orthogonal auf
auf der roten Strecke liegen, orthogonal auf ![]() projiziert (grüne Punkte).
projiziert (grüne Punkte).
Die Länge der Strecken auf der Projektionsgerade kann nur zwei Werte annehmen (entsprechend der Projektion der Kanten des Einheitsquadrates). Deshalb können wir von einer „angeordneten Struktur“ sprechen.
Bewegt man sich entlang der Geraden, wirkt die Folge dieser Werte mehr oder weniger willkürlich angeordnet – es gibt keine Translationssymmetrie. Erweitern wir aber das Universum auf zwei Dimensionen wird alles plötzlich klar: Der Quasikristall ist nur Teil der Projektion eines regelmäßigen Quadratgitters. Die Vergrößerung der Dimension lässt zu, dass wir die versteckten Strukturen des Quasikristalls verstehen.
Dieser Prozess lässt sich auch auf höhere Dimensionen verallgemeinern. Sehr anschaulich erläutert z. B. Senechal (1995) die Gesetzmäßigkeiten und Annahmen für Projektionsmethoden und Mehrgittermethoden, die zu quasikristallinen Punktmengen führen. Projiziert man beispielsweise Teile des fünfdimensionalen Würfelgitters (![]() ) auf eine bestimmte Ebene, so erhält man eine Punktmenge, die im obigen Sinne als zweidimensionaler Quasikristall bezeichnet werden kann. Die Punktmenge selbst bildet die Eckpunkte einer Pflasterung der Ebene mit Penrose-Rauten (mit ihren zwei charakteristischen Elementarbausteinen, vgl. Abschnitt 2 und Abbildung 4.1).
) auf eine bestimmte Ebene, so erhält man eine Punktmenge, die im obigen Sinne als zweidimensionaler Quasikristall bezeichnet werden kann. Die Punktmenge selbst bildet die Eckpunkte einer Pflasterung der Ebene mit Penrose-Rauten (mit ihren zwei charakteristischen Elementarbausteinen, vgl. Abschnitt 2 und Abbildung 4.1).
6. Schlussfolgerung
Wir haben einen Weg entdeckt, wie Mathematiker arbeiten. Dies wird manchmal mit Hilfe des folgenden Satzes zusammengefasst:
Wenn man etwas nicht versteht, versucht man den Blickwinkel zu ändern. Es kann durchaus sein, dass der neue Blickwinkel eine Erklärung für bisher versteckte Strukturen liefert. Dies tut man bereits dann, wenn man versucht einen Kegel zu verstehen: Man wählt ein geeignetes Koordinatensystem, in dem die Darstellung einfach ist und die Eigenschaften des Kegels deutlich hervortreten.
Die Arbeit mit Objekten höherer Dimension kann die Vorstellungen und die mathematischen Konzepte der Schüler auf vielfältige Weise bereichern.
Insbesondere können die Schüler
- ihr Wissen über Projektionen dreidimensionaler Objekte auf eine Ebene auffrischen und wiederholen;
- Analogien nutzten, um ihr Wissen, ausgehend von der vertrauten dreidimensionalen Welt, zu erweitern;
- einen ersten Einblick in die Bedeutung höherer Dimensionen erhalten;
- die unterschiedlichen Zugangsmöglichkeiten zu Objekten höherer Dimension kennen lernen;
- Eigenschaften von Objekten dieser Welt auf abstrakte Weise beschreiben und im Rahmen ihres Gültigkeitsbereichs nutzen lernen;
Literaturhinweise
[1] BOTELHO, L.; BOTELHO, R.: Quantum Geometry of bosonic strings – Revisited. Notas de Física, Centro Brasileira de Pesquisas Físicas (1999).
[2] CAYLEY, A.: On Jacobi’s elliptic functions, in reply to the Rev..; and on quaternions. Philosophical Magazine. (1845) Nr. 26, S. 208–211.
[3] DELONE B.N., Geometry of positive quadratic forms, Usp. Mat. Nauk 3 (1937), S. 16‐62, und Usp. Mat. Nauk 4 (1938), S. 102‐164. (Russisch)
[4] GRAUMANN, G.: Spate in drei und mehr Dimensionen. MU 55/1 (2009), S. 16‐25
[5] HAMILTON, W. R.: On quaternions, or an new system of imagineries in algebra. Philosophical Magazine.(1844) Bd. 25(3), S. 489‐495.
[6] LAGARIAS, J.: Meyer’s concept of quasicrystal and quasiregular sets. Community of Mathematical Physics 179 (1996), S. 365‐376.
[7] MEYER, Y.: Algebraic numbers and harmonic analysis. North Holland (1972)
[8] RIEMANN, B.: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe (Habil.). Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, Bd. 13 (1868)
[9] RUPPERT, M.: Würfelbetrachtungen. Drei Wege zu höheren Dimensionen. MU 56/1 (2010), S. 34‐53.
[10] SCHLÄFLI, L.: Theorie der vielfachen Kontinuität (1852). Denkschrift der Schweizerischen Naturforschenden Gesellschaft, Bd. 38, 1., Hrsg. Graf, J. H. (1901), S. 1‐237.
[11] SENECHAL, M.: Quasicrystals and geometry. Cambridge University Press (1995)
Die Entwicklung des Konzepts einer „höherdimensionalen Geometrie“ begann mit den wissenschaftlichen Arbeiten von Hamilton (1844), Cayley (1845), Schläfli (1852) und Riemann (1868).
Autors: Markus Ruppert und Hans-Georg Weigand.
Weitere Klein-Artikel in in anderen Sprachen verfügbar: Englisch, Französisch, …
Andere Sprachen: Englisch, Französisch, Italienisch, Arabisch, Khmer

 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português
Hi I am so glad I found your weblog, I really found you by error, while I was looking on Aol for something else, Anyhow I am here now and would just like to say cheers for a tremendous post and a all round