 Autorin: Christiane Rousseau.
Autorin: Christiane Rousseau.
Wie kann man gleich große Kugeln möglichst platzsparend auf- und nebeneinander legen? Kepler vermutete, dass die dichteste Kugelpackung diejenige ist, die man beim Obsthändler am Orangenstand sieht und die kubisch flächenzentriertes Gitter (Abb. 1) genannt wird. Auf dem Internationalen Mathematiker-Kongress im Jahr 1900 formulierte David Hilbert 23 Probleme, deren Lösung den Fortschritt der mathematischen Wissenschaft im 20. Jahrhundert stark beeinflussen würde. Das Problem der dichtesten Kugelpackung, auch Keplersche Vermutung genannt, ist ein Teil von Hilberts 18. Problem. Die Keplersche Vermutung wurde 1998 von Thomas Hales bewiesen. Details dieses Beweises wurden allerdings erst 2006 veröffentlicht.
1. Wie gehen wir mit derartigen Problemen um?
Wir betrachten verschiedene Anordnungen von gleichgroßen Kugeln im Raum und berechnen in jedem Fall die Dichte der Anordnung, also den Anteil des von den Kugeln eingenommen Volumens am Gesamtvolumen. Wir nennen ![]() die größte Dichte einer Kugelpackung in der
die größte Dichte einer Kugelpackung in der ![]() -ten Dimension. Natürlich hängt diese Dichte von der Form des umgrenzenden Bereiches ab. Um dies zu verhindern, betrachten wir sehr große Bereiche, so dass Randeffekte vernachlässigbar sind. Kepler vermutete 1611, dass die dichteste Kugelpackung diejenige ist, die man bei Orangen auf einem Obstmarkt beobachten kann. Warum dauerte es also so lange, bis diese Vermutung bewiesen war? Das Problem ist, dass es unendlich viele mögliche Anordnungen von Kugeln gibt. Von jeder einzelnen Anordnung können wir nachweisen, dass ihre Dichte kleiner oder gleich der auf dem Obstmarkt zu beobachtenden ist. Das Problem ist aber, dass wir nur endlich viele Anordnungen beschreiben können. Die Dichte bei einer Anordnung zu berechnen kann sehr schwierig oder unmöglich werden, wenn sich Teile der Anordnung nicht wiederholen, also kurz gesagt, wenn die Anordnung nicht periodisch ist.
-ten Dimension. Natürlich hängt diese Dichte von der Form des umgrenzenden Bereiches ab. Um dies zu verhindern, betrachten wir sehr große Bereiche, so dass Randeffekte vernachlässigbar sind. Kepler vermutete 1611, dass die dichteste Kugelpackung diejenige ist, die man bei Orangen auf einem Obstmarkt beobachten kann. Warum dauerte es also so lange, bis diese Vermutung bewiesen war? Das Problem ist, dass es unendlich viele mögliche Anordnungen von Kugeln gibt. Von jeder einzelnen Anordnung können wir nachweisen, dass ihre Dichte kleiner oder gleich der auf dem Obstmarkt zu beobachtenden ist. Das Problem ist aber, dass wir nur endlich viele Anordnungen beschreiben können. Die Dichte bei einer Anordnung zu berechnen kann sehr schwierig oder unmöglich werden, wenn sich Teile der Anordnung nicht wiederholen, also kurz gesagt, wenn die Anordnung nicht periodisch ist.
Das Problem der dichtesten Kugelpackung existiert in allen Dimensionen. Schon 1890 wurde es für zweidimensionale Kugeln – also Kreisscheiben – gelöst. Mit Kugelpackungen in höheren Dimensionen können fehlerkorrigierende Verschlüsselungsverfahren konstruiert werden. Bereits in der zweiten Dimension stoßen wir aber auf die zwei oben genannten Schwierigkeiten: Nicht alle Anordnungen können gezählt werden, und zudem existieren nicht periodische Anordnungen.
Im Folgenden zeigen wir, wie wir mit diesen Schwierigkeiten umgehen, und dass die Abb. 2(b) die dichteste Packung veranschaulicht. Weiterhin erläutern wir, warum es schwierig ist, den Beweis auf drei Dimensionen zu verallgemeinern. Einige Bemerkungen zum Problem in höheren Dimensionen beenden unsere Erläuterungen.
2. Der zweidimensionale Fall
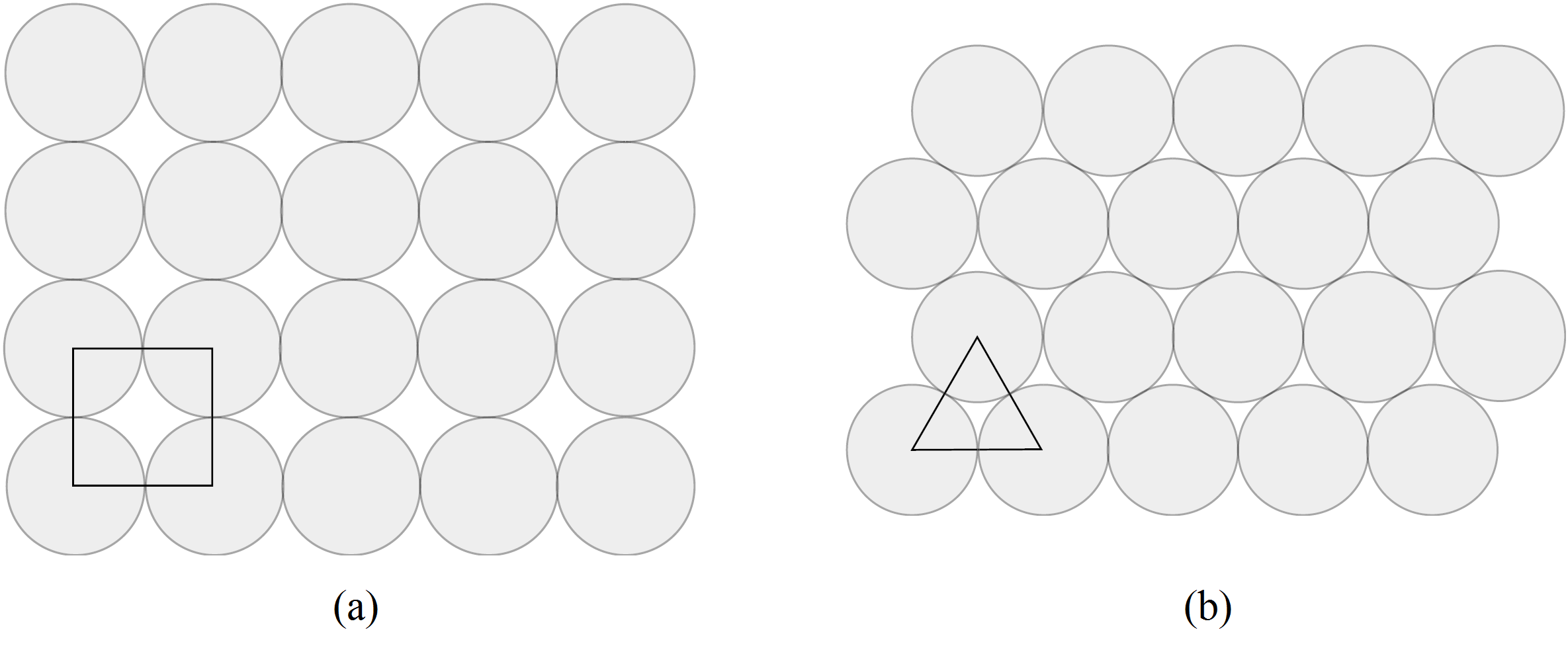
Betrachten Sie die zwei „Packungen“ der Kreisscheiben in Abb. 2. Als leichte Übung berechnen wir den Anteil der von den Kreisscheiben bedeckten Fläche an der Fläche eines jeden Quadrats bzw. an der Fläche eines jeden Dreiecks. Die Anordnung in (b) ist dichter als die in (a), da für die Dichte in (b) gilt ![]() , aber die Dichte in (a) nur
, aber die Dichte in (a) nur ![]() beträgt. Von jeder periodischen Packung können wir zeigen, dass diese eine kleinere Dichte hat als die Packung in Abb. 2(b).
beträgt. Von jeder periodischen Packung können wir zeigen, dass diese eine kleinere Dichte hat als die Packung in Abb. 2(b).
Aber wie können wir dies zeigen?
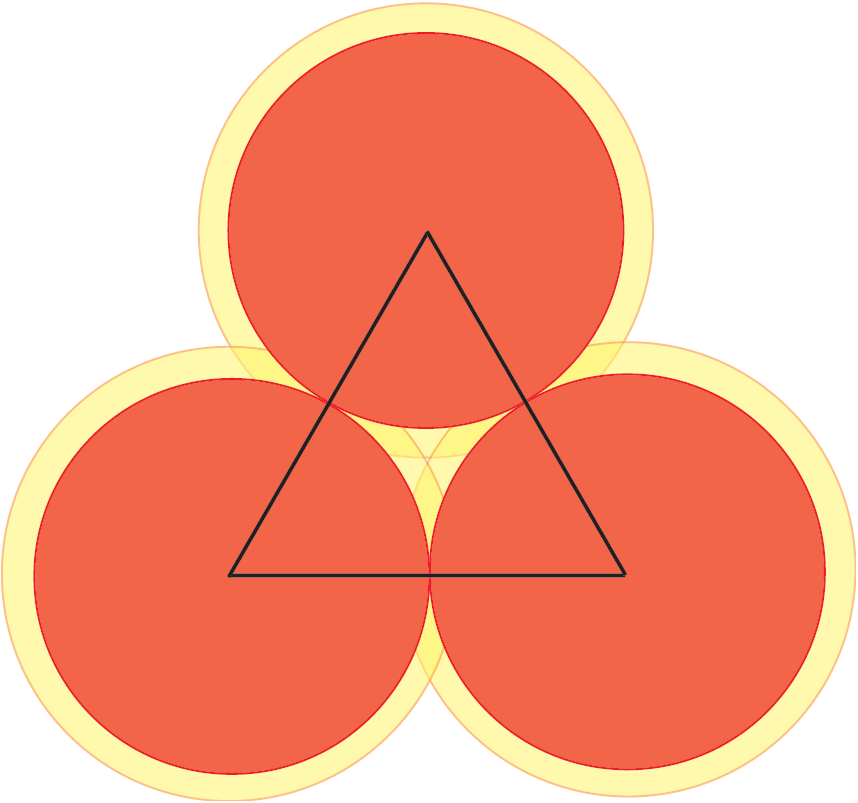
Die Beweisidee wurde schon 1890 von dem norwegischen Mathematiker Axel Thue gefunden. Wir teilen die Ebene in beschränkte Bereiche auf und zeigen, dass in allen Bereichen die Dichte kleiner gleich ![]() ist. Abb. 3. zeigt drei Kreisscheiben – rot angefärbt – die nicht näher beieinander liegen können. Jetzt betrachten wir das Dreieck mit den Ecken in den Mittelpunkten der Kreise. In diesem Dreieck liegt eine kleine, von Kreisscheiben nicht bedeckte Fläche. Wenn wir jedoch die Kreisscheiben mit dem Faktor
ist. Abb. 3. zeigt drei Kreisscheiben – rot angefärbt – die nicht näher beieinander liegen können. Jetzt betrachten wir das Dreieck mit den Ecken in den Mittelpunkten der Kreise. In diesem Dreieck liegt eine kleine, von Kreisscheiben nicht bedeckte Fläche. Wenn wir jedoch die Kreisscheiben mit dem Faktor ![]() vergrößern, dann füllen die vergrößerten Scheiben das Dreieck aus. Der Faktor
vergrößern, dann füllen die vergrößerten Scheiben das Dreieck aus. Der Faktor ![]() ist der kleinste, um dieses Ziel zu erreichen.
ist der kleinste, um dieses Ziel zu erreichen.
Wir werden nun die folgende Idee benutzen, um die Ebene in passende Bereiche zu unterteilen. Wir betrachten die (nicht lückenlose) Überdeckung der Ebene mit Kreisscheiben vom Radius ![]() . Jede Kreisscheibe betten wir in eine Kreisscheibe mit gleichem Mittelpunkt und Radius
. Jede Kreisscheibe betten wir in eine Kreisscheibe mit gleichem Mittelpunkt und Radius ![]() , die wir eine großen Kreisscheibe nennen. Nun können wir unsere drei Bereiche beschreiben. Der erste Bereich ist das Komplement der Vereinigung der großen Kreisscheiben. Offensichtlich ist die Dichte dieses Bereichs
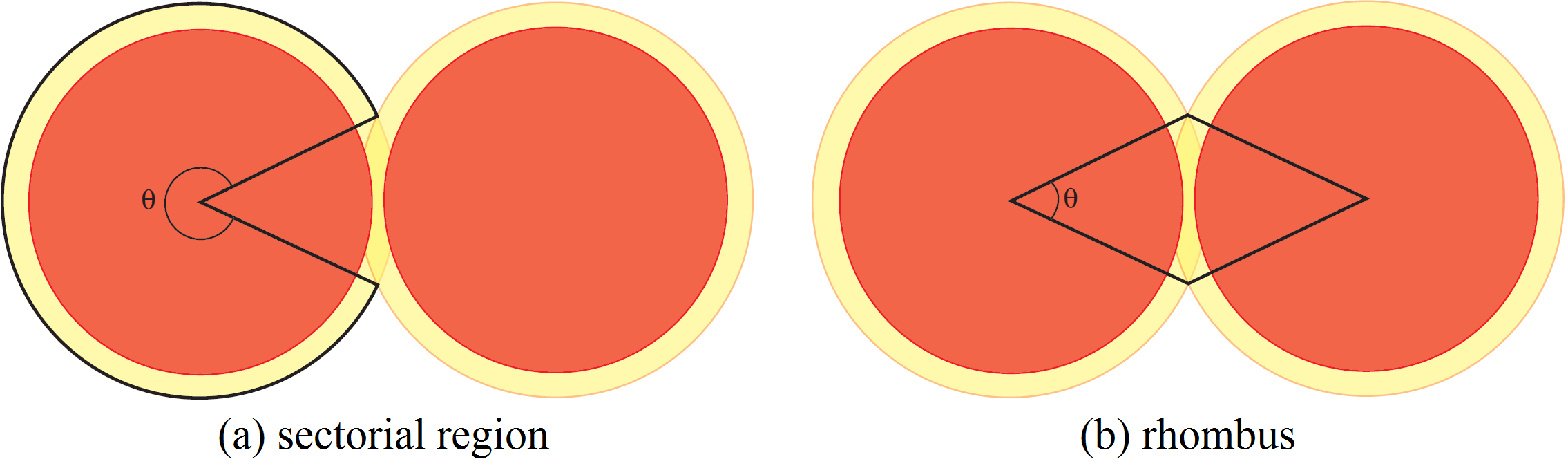
, die wir eine großen Kreisscheibe nennen. Nun können wir unsere drei Bereiche beschreiben. Der erste Bereich ist das Komplement der Vereinigung der großen Kreisscheiben. Offensichtlich ist die Dichte dieses Bereichs ![]() . Je nach Entfernung der Scheibenmitten überlappen sich die großen Kreisscheiben oder nicht. Wenn sie sich überlappen, dann schneiden sich ihre Randkreise. Wir verbinden diese Schnittpunkte mit den Mittelpunkten der Scheiben und teilen somit die großen Kreisscheiben in Sektoren. Es gibt zwei Arten von Sektoren:
. Je nach Entfernung der Scheibenmitten überlappen sich die großen Kreisscheiben oder nicht. Wenn sie sich überlappen, dann schneiden sich ihre Randkreise. Wir verbinden diese Schnittpunkte mit den Mittelpunkten der Scheiben und teilen somit die großen Kreisscheiben in Sektoren. Es gibt zwei Arten von Sektoren:
- Bereiche, in denen die große Kreisscheibe keine andere große Kreisscheibe schneidet (Abb. 4(a)). In diesen Bereichen ist die Dichte
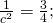
- Bereiche, in denen sich die großen Kreisscheiben überlappen – wie in Abb. 4(b). Wir fassen diese Bereiche als Paare – wie in der Abb. 4(b) – zu einer Raute zusammen. Somit müssen wir nur die Dichte innerhalb der Raute berechnen. Da die Entfernung der Kreismittelpunkte mindestens
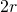 beträgt, weil die Scheiben sich nicht schneiden, berechnet sich das maximale Winkelmaß der Sektoren zu
beträgt, weil die Scheiben sich nicht schneiden, berechnet sich das maximale Winkelmaß der Sektoren zu 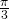 . Sei
. Sei 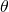 das Winkelmaß eines Sektors. Die Dichte innerhalb der Raute hängt von
das Winkelmaß eines Sektors. Die Dichte innerhalb der Raute hängt von 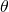 ab; Sie ist der Quotient aus der Summe der Flächeninhalte der zwei Kreissektoren und dem Flächeninhalt der Raute. Jeder Sektor eines Kreises hat die Fläche
ab; Sie ist der Quotient aus der Summe der Flächeninhalte der zwei Kreissektoren und dem Flächeninhalt der Raute. Jeder Sektor eines Kreises hat die Fläche 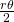 . Folglich ist die Fläche innerhalb der Raute, die durch die Kreisscheiben überdeckt wird
. Folglich ist die Fläche innerhalb der Raute, die durch die Kreisscheiben überdeckt wird 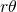 . Den Flächeninhalt einer Raute mit der Seite
. Den Flächeninhalt einer Raute mit der Seite 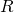 und dem Winkels
und dem Winkels 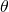 beträgt
beträgt 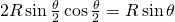 . Folglich ist die Dichte
. Folglich ist die Dichte 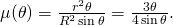 Um einen Extremwert zu finden, genügt es, den Funktionsterm
Um einen Extremwert zu finden, genügt es, den Funktionsterm 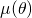 im Intervall
im Intervall ![Rendered by QuickLaTeX.com [0,\frac{\pi}3]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-97108dd255a2234a8ad4dd9ed1cb498f_l3.png) zu betrachten. Er nimmt sein Maximum
zu betrachten. Er nimmt sein Maximum 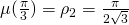 an der Stelle
an der Stelle 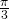 an, weil gilt
an, weil gilt 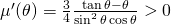 für
für 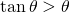 .
.
Da dieser Beweis sehr elegant ist, betrachten wir einige Merkmale im Detail. Die beste Dichte ist ![]() . Dies ist auch die beste Dichte in jedem Gebiet der Ebene, das wir betrachtet haben.
. Dies ist auch die beste Dichte in jedem Gebiet der Ebene, das wir betrachtet haben.
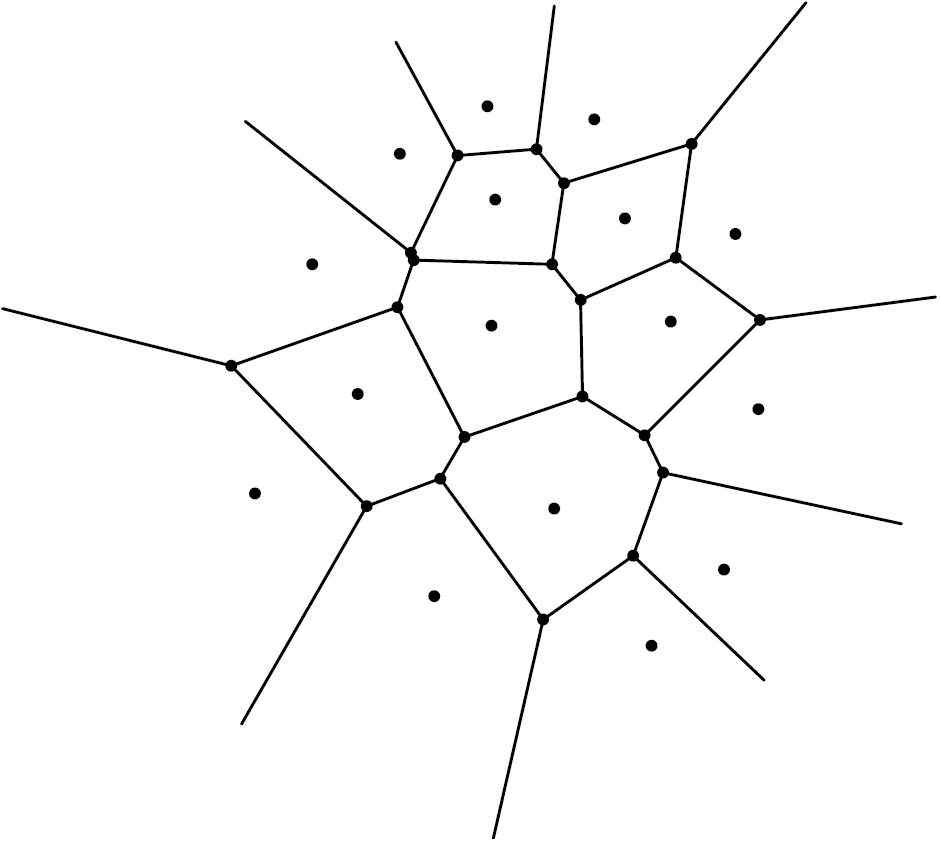
Es gibt noch einen Weg, um die Ebene in Bereiche zu zerlegen. Diesen beschreibt das Voronoi-Diagramm der Menge der Scheibenmitten. Betrachtet man eine Menge ![]() von Punkten in einer Ebene, so ist das Voronoi-Diagramm von
von Punkten in einer Ebene, so ist das Voronoi-Diagramm von ![]() die Zerlegung der Ebene in Bereiche, von denen jeder zu einem Punkt
die Zerlegung der Ebene in Bereiche, von denen jeder zu einem Punkt ![]() von
von ![]() gehört, so dass der zu einem gegebenen Punkt
gehört, so dass der zu einem gegebenen Punkt ![]() gehörende Bereich die Punkte der Ebene enthält, die näher zu
gehörende Bereich die Punkte der Ebene enthält, die näher zu ![]() als zu einem anderen Punkt
als zu einem anderen Punkt ![]() von
von ![]() liegen. Diese Gebiete werden Voronoi-Zellen genannt. Da die Mittelsenkrechte einer Strecke
liegen. Diese Gebiete werden Voronoi-Zellen genannt. Da die Mittelsenkrechte einer Strecke ![]() der geometrische Ort der Punkte ist, die gleich weit von
der geometrische Ort der Punkte ist, die gleich weit von ![]() und
und ![]() entfernt sind, wird das Voronoi-Diagramm von Punkten gebildet, wie sie in Figur 5 dargestellt sind. Die gemeinsame Seite zwischen einem Paar benachbarter Voronoi-Zellen besteht aus einer Strecke, die auf der Mittelsenkrechten zu zwei benachbarten Punkten von
entfernt sind, wird das Voronoi-Diagramm von Punkten gebildet, wie sie in Figur 5 dargestellt sind. Die gemeinsame Seite zwischen einem Paar benachbarter Voronoi-Zellen besteht aus einer Strecke, die auf der Mittelsenkrechten zu zwei benachbarten Punkten von ![]() liegt.
liegt.
Bei einer Packung aus Kreisscheiben in der Ebene betrachten wir das Voronoi-Diagramm der Kreiszentren. In Abb. 2 (a) sind die Voronoi-Zellen Quadrate, rechts sind es Sechsecke. Die Dichte jedes Kreises innerhalb der sechseckigen Voronoi-Zelle ist gleich ![]() . Wenn wir eine gegebene Scheibe mit sich nicht überschneidenden Scheiben des gleichen Radius umgeben, so ist die Voronoi-Zelle mit minimalem Flächeninhalt das umbeschriebene regelmäßige Sechseck.
. Wenn wir eine gegebene Scheibe mit sich nicht überschneidenden Scheiben des gleichen Radius umgeben, so ist die Voronoi-Zelle mit minimalem Flächeninhalt das umbeschriebene regelmäßige Sechseck.
3. Der dreidimensionale Fall
3.1. Die Schwierigkeit des Problems
Es ist naheliegend, das Vorgehen des zwei- auf den dreidimensionalen Fall zu übertragen. Das Voronoi-Diagramm kann man wie zuvor definieren. Seine begrenzten Zellen sind konvexe Polyeder. Um eine Kugel kann man zwölf Kugeln gleichen Radius setzen, wobei im Unterschied zum ebenen Fall noch freier Raum bleibt. Wir können aber versuchen, ob wir die ![]() Kugeln versetzen und eine
Kugeln versetzen und eine ![]() . Kugel einschieben können. Thomas Hales bewies, dass eine solche Anordnung nicht existiert. Nun gibt es viele verschiedene Möglichkeiten
. Kugel einschieben können. Thomas Hales bewies, dass eine solche Anordnung nicht existiert. Nun gibt es viele verschiedene Möglichkeiten ![]() Kugeln um eine gegebene Kugel zu platzieren, und alle erzeugen unterschiedliche Voronoi-Zellen desselben Volumens! Die optimale Anordnung, um das Volumen der Voronoi-Zelle zu minimieren, entsteht, wenn die
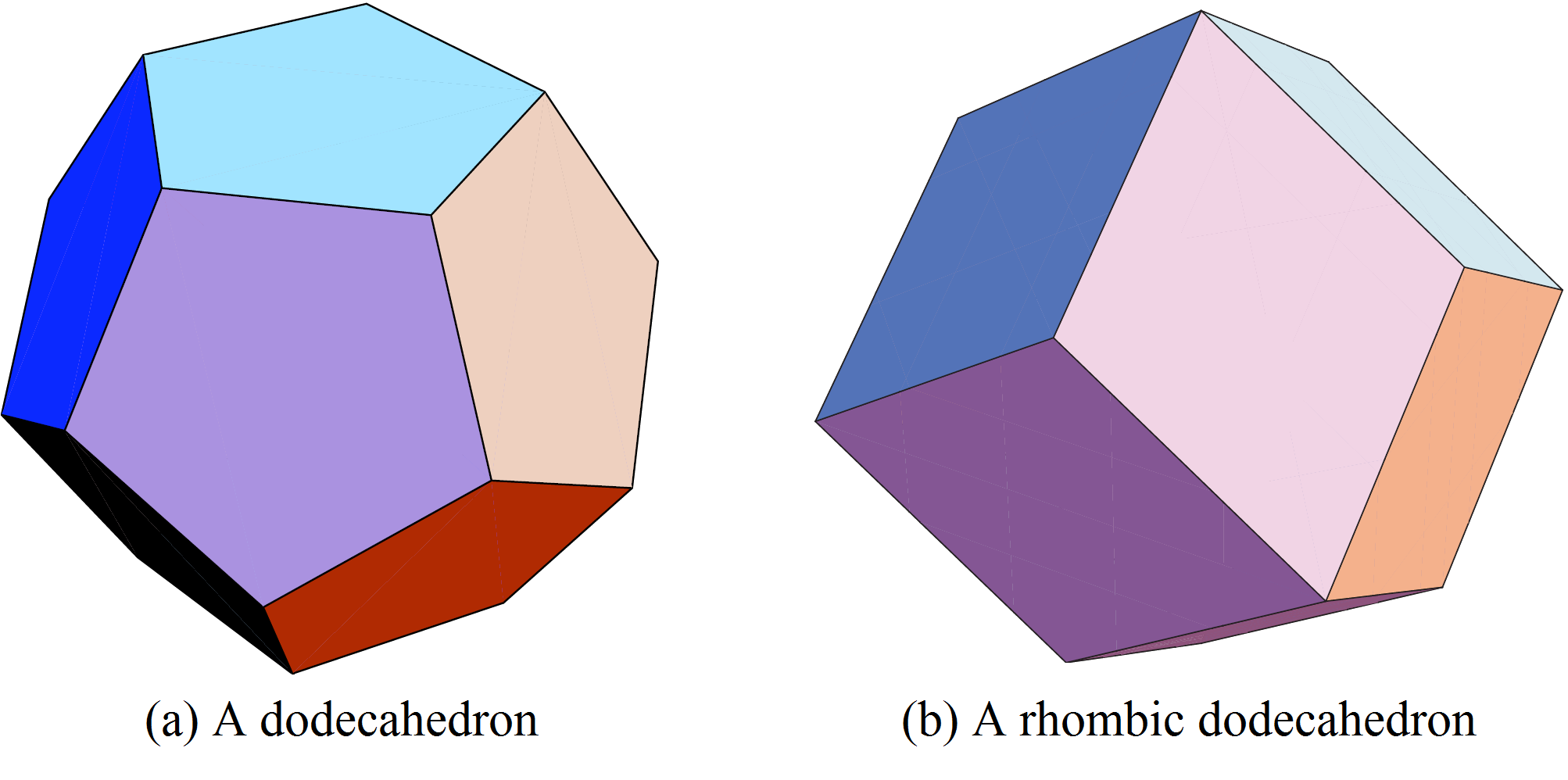
Kugeln um eine gegebene Kugel zu platzieren, und alle erzeugen unterschiedliche Voronoi-Zellen desselben Volumens! Die optimale Anordnung, um das Volumen der Voronoi-Zelle zu minimieren, entsteht, wenn die ![]() Kugeln die Ausgangskugel in den Ecken eines einbeschriebenen Dodekaeders (s. Abb. 6(a)) berühren. Diese Lage sagte Fejes Tóth schon um 1940 voraus, aber erst 1999 bewies sie der Bachelor-Student Sean McLaughlin.
Kugeln die Ausgangskugel in den Ecken eines einbeschriebenen Dodekaeders (s. Abb. 6(a)) berühren. Diese Lage sagte Fejes Tóth schon um 1940 voraus, aber erst 1999 bewies sie der Bachelor-Student Sean McLaughlin.
Also ist die Voronoi-Zelle der gegebenen Kugel ein zu der Kugel einbeschriebenes Dodekaeder.
Die Dichte der Kugel innerhalb ihrer Voronoi-Zelle ist berechenbar. Sie ist schlechter als die Dichte beim Verpacken von Orangen auf einem Obstmarkt! Deshalb stellt sich die Frage, ob wir es besser machen können? Die Antwort wird allerdings „nein“ sein.
Weil es unmöglich ist, den Raum mit sich nicht überschneidenden regelmäßigen Dodekaedern lückenlos zu füllen, bleiben Leerräume zwischen ihnen. Somit sehen wir, dass der dreidimensionale Fall viel schwerer als der zweidimensionale Fall zu lösen ist, da die lokale optimale Lösung nicht mit der globalen optimalen Lösung übereinstimmt.
Für die optimale Lösung, deren Geometrie wir im nächsten Abschnitt studieren werden, sind die Zentren der Kugeln in den Ecken des kubisch-flächenzentrierten Gitters platziert. Die dazugehörigen Voronoi-Zellen sind Rhombendodekaeder (siehe Abb. 6(b)).
Rhombendodekaeder pflastern den Raum lückenlos. Solche Pflasterungen kennt man aus der Kristallographie.
Den Beweis, dass diese Packung bestmöglich ist, fanden 1998 Thomas Hales und sein Master-Student Samuel Ferguson – ein vollständiger Beweis wurde 2006 veröffentlicht. Dieser computerunterstützte Beweis ist schwierig und aufwändig. Obwohl wir den Beweis des zweidimensionalen Falls nicht imitieren können, bleibt die Idee dieselbe: Der Raum wird in Bereiche zerlegt, die endlich viele Typen aufweisen. Dann wird die Dichte der Bereiche berechnet – nach Typen aufgeschlüsselt. Das lange Programm ist im Internet verfügbar für die, die es studieren oder überprüfen wollen.
3.2. Die Geometrie der optimalen Packung
Stellen Sie sich eine Pflasterung des dreidimensionalen Raumes mit Würfeln vor. Nun denken wir uns je eine Kugel mit ihrem Mittelpunkt in jeder Würfelecke und je eine Kugel in den
Mittelpunkten der ![]() Würfelflächen (s. Abb. 7).
Würfelflächen (s. Abb. 7).
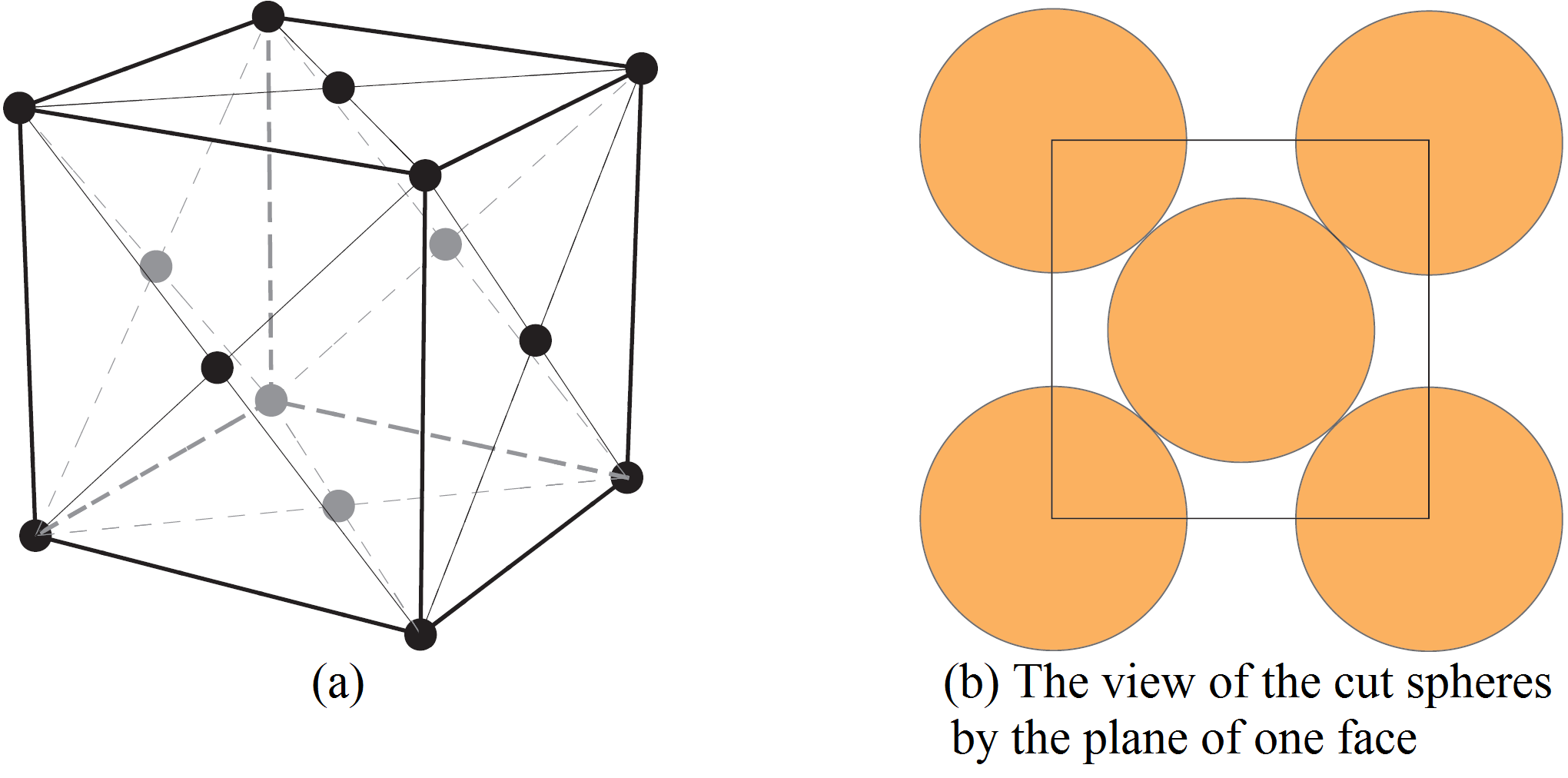
Abb. 7: Links: Die Mittelpunkte der Kugeln im kubisch-flächenzentrierten Gitter
Rechts: Schnitt durch eine Seitenfläche des Würfels
Wir wählen den Radius der Kugeln so groß wie möglich, ohne dass sich die Kugeln schneiden. Wenn ![]() die Länge einer Würfelkante ist, dann liefert Abb. 7 den Radius der Kugeln als
die Länge einer Würfelkante ist, dann liefert Abb. 7 den Radius der Kugeln als ![]() . Ein Achtel jeder Kugel um eine Würfelecke liegt im Inneren des Würfels. Da es acht Ecken gibt, addieren sich die Achtel zu dem Volumen einer Kugel. Die Hälfte jeder in einem Flächenmittelpunkt des Würfels zentrierten Kugel liegt im Inneren des Würfels. Da ein Würfel sechs Flächen hat, addieren sich die Hälften zu dem Volumen der drei Kugeln. Daher ist die Dichte das Volumen der vier Kugeln geteilt durch das Volumen des Würfels. Das Volumen jeder Kugel ist
. Ein Achtel jeder Kugel um eine Würfelecke liegt im Inneren des Würfels. Da es acht Ecken gibt, addieren sich die Achtel zu dem Volumen einer Kugel. Die Hälfte jeder in einem Flächenmittelpunkt des Würfels zentrierten Kugel liegt im Inneren des Würfels. Da ein Würfel sechs Flächen hat, addieren sich die Hälften zu dem Volumen der drei Kugeln. Daher ist die Dichte das Volumen der vier Kugeln geteilt durch das Volumen des Würfels. Das Volumen jeder Kugel ist ![]() und das Volumen des Würfels ist
und das Volumen des Würfels ist ![]() . Also ist die Dichte
. Also ist die Dichte
![]()
Wie wird diese Anordnung erreicht? Man kann das mit dem Stapeln von Orangen vergleichen: Wir legen die erste ebene Schicht aus Kugeln wie in Abb. 2 (b). Darauf legen wir eine zweite Schicht, die leicht gegenüber der darunter liegenden Schicht verschoben ist, z.B. nach oben rechts. Die dritte Schicht liegt auf der zweiten Schicht mit einer Verschiebung in dieselbe Richtung, usw. Jetzt ist aber zu überlegen: Können wir die Richtung der Verschiebung zwischen den verschiedenen Schichten verändern, ohne die Dichte zu verändern? Ja, das können wir, aber das dazugehörige Gitter der Mittelpunkte ist nicht mehr das kubisch-flächenzentrierte. Somit ist die Packung mit der größten Dichte nicht eindeutig bestimmt.
Es ist nicht offensichtlich, dass das vertraute Aufeinandersetzen der Orangen dem kubisch-flächenzentrierten Gitter entspricht. In der Abb. 7 sehen wir zueinander orthogonale Geraden , auf denen die Mittelpunkte der Kugeln aufgereiht sind. Es ist eine gute Visualisierungsübung festzustellen, dass diese Geraden wirklich bei der Stapelung von Orangen vorkommen, dass aber keine in waagrechten Ebenen liegt. Die Ebene in Abb. 2 (b) ist eine geneigte Ebene durch die Mittelpunkte dreier Würfelflächen mit gemeinsamer Ecke (s. Abb. 77 (a). Die Abb. 8 soll eine Packung aus vier übereinanderliegenden Schichten wie in Abb. 2(b ) verdeutlichen. Die zwei Geraden durch die Kugelmittelpunkte stehen im Raum aufeinander senkrecht.
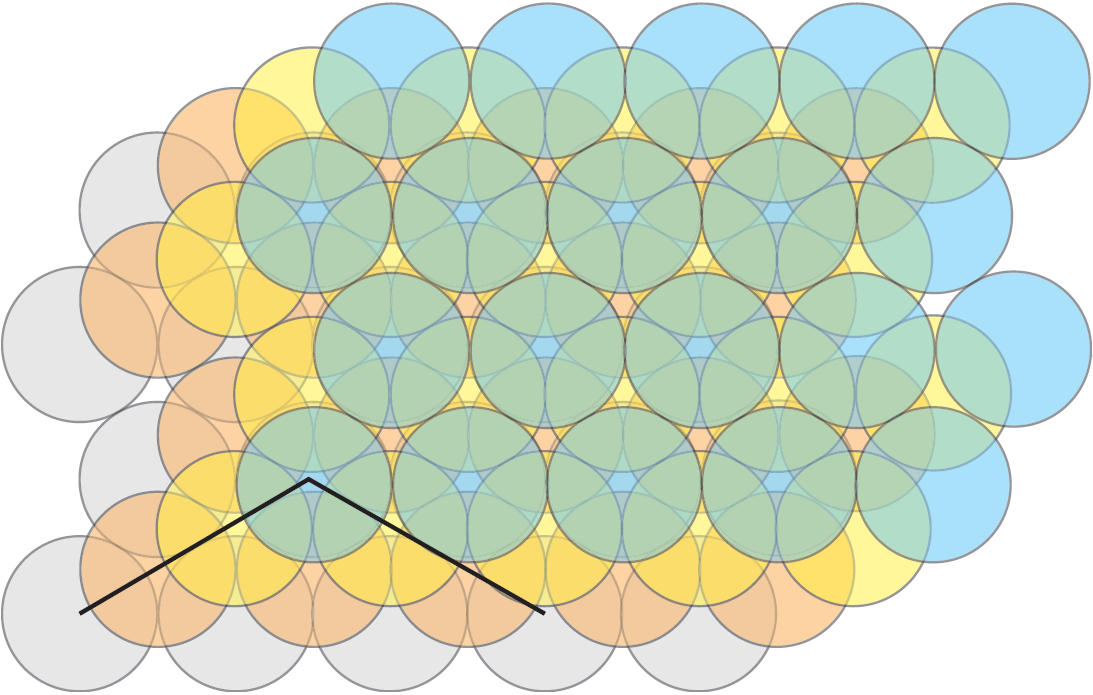
Abb. 8: Vier übereinanderliegende Kugelschichten wie in Abb. 2(b) und zwei zueinander senkrechte Geraden durch passende Mittelpunkte
4. Ausblicke
4.1. Anwendungen in der Kristallographie
Die Frage nach der dichtesten Kugelpackung richtete Thomas Harriot an Johannes Kepler am Ende des 16. Jahrhunderts. Schon damals glaubte Harriot an die Existenz von Atomen und suchte nach deren gegenseitiger Anordnung. Wenn Atome in einem Material gleichmäßig angeordnet sind, sprechen Chemiker von einem Kristall. Schwere Materialien, wie z.B. Metalle, haben oft Atome, die um die Punkte des kubisch-flächenzentrierten Gitters angeordnet sind. Andere gleichmäßige Anordnungen geringerer Dichte existieren ebenfalls. Eine gleichmäßige Anordnung mit geringerer Dichte ist die Würfelpackung, in der Atome an den Ecken von Würfeln angeordnet sind. Es gibt nur ein chemisches Element mit dieser Anordnung von Atomen, nämlich das radioaktive Polonium. ( Für Einzelheiten s. [4].)
4.2. Zufällige Packungen
Wenn man vorsichtig seine Orangen in große Schachteln verpackt und sie im oben beschriebenen kubisch-flächenzentrierten Gitter anordnet, bekommt man die Dichte ![]() Welche Dichte entsteht aber, wenn man die Orangen schnell und willkürlich in eine Schachtel wirft? Dann entsteht das, was eine zufällig lose Packung genannt wird. Natürlich wechselt dann die Dichte. Wenn man die Schachtel schüttelt, wird man wahrscheinlich die Dichte vergrößern. Aber was ist die größte Dichte? Experimente belegen, dass die Dichte zwischen
Welche Dichte entsteht aber, wenn man die Orangen schnell und willkürlich in eine Schachtel wirft? Dann entsteht das, was eine zufällig lose Packung genannt wird. Natürlich wechselt dann die Dichte. Wenn man die Schachtel schüttelt, wird man wahrscheinlich die Dichte vergrößern. Aber was ist die größte Dichte? Experimente belegen, dass die Dichte zwischen ![]() % (zufällig lose Packung) und einem Maximum von
% (zufällig lose Packung) und einem Maximum von ![]() % (zufällige enge Packung) variiert. Im Jahr 2008 wiesen Song, Wang und Maske in einem Brief an das Magazin Nature diese Grenze n nach [3].
% (zufällige enge Packung) variiert. Im Jahr 2008 wiesen Song, Wang und Maske in einem Brief an das Magazin Nature diese Grenze n nach [3].
Hinweis: Die Beschreibungen „zufällig lose“ bzw. „enge Packung“ finden sich in Fejes L. Toth, Reguläre Figuren, Teubner Verl., Leipzig 1965, S. 285.
4.3. Packungen aus Objekten, die keine Kugeln sind
Es lässt sich eine höhere Dichte als ![]() erreichen, wenn man z.B. die Form der identischen Objekte von Kugeln zu Ellipsoiden verändert. In [1] wird bewiesen, dass die Dichte zufällig enger Packungen aus Sphäroiden-mit einem Achsenverhältnis wie etwa bei M&M-Bonbons zwischen
erreichen, wenn man z.B. die Form der identischen Objekte von Kugeln zu Ellipsoiden verändert. In [1] wird bewiesen, dass die Dichte zufällig enger Packungen aus Sphäroiden-mit einem Achsenverhältnis wie etwa bei M&M-Bonbons zwischen ![]() und
und ![]() liegt, während die Dichte bei Ellipsoiden mit anderen Achsenverhältnissen bis
liegt, während die Dichte bei Ellipsoiden mit anderen Achsenverhältnissen bis ![]() wachsen kann. An den Dichten zufälliger Packungen sind Industriebetriebe interessiert, z. B. wenn das Verpacken von identischen Objekten (z.B. Bonbons oder pharmazeutische Tabletten) automatisiert wird. Insbesondere kann sich die Dichte während des Transports verändern.
wachsen kann. An den Dichten zufälliger Packungen sind Industriebetriebe interessiert, z. B. wenn das Verpacken von identischen Objekten (z.B. Bonbons oder pharmazeutische Tabletten) automatisiert wird. Insbesondere kann sich die Dichte während des Transports verändern.
4.4. Ein Wort zu höheren Dimensionen
In höheren Dimensionen sind die dichtesten regulären Packungen aus Hypersphären bis zur ![]() . Dimension bekannt, sehr wenig weiß man dagegen über nicht reguläre Packungen. Mit Kugelpackungen in höheren Dimensionen kann man fehlerkorrigierende Verschlüsselungen konstruieren. Deren Wirkungsweise besteht darin, Buchstaben oder Wörter durch Symbolsequenzen zu ersetzen, die Codewörter genannt werden, und von denen sich eines vom anderen durch mindestens
. Dimension bekannt, sehr wenig weiß man dagegen über nicht reguläre Packungen. Mit Kugelpackungen in höheren Dimensionen kann man fehlerkorrigierende Verschlüsselungen konstruieren. Deren Wirkungsweise besteht darin, Buchstaben oder Wörter durch Symbolsequenzen zu ersetzen, die Codewörter genannt werden, und von denen sich eines vom anderen durch mindestens ![]() Buchstaben unterscheidet. Wenn dann weniger als
Buchstaben unterscheidet. Wenn dann weniger als ![]() Fehler in der Übertragung eines Codewortes auftreten, existiert höchstens ein Codewort in einem kleineren Abstand als
Fehler in der Übertragung eines Codewortes auftreten, existiert höchstens ein Codewort in einem kleineren Abstand als ![]() von dem gerade betrachteten Wort, so dass eine Korrektur möglich ist. In den Fehlerkorrekturcodes, die auf Kugelpackungen beruhen, wandelt man die Verschlüsselungszeichen in Koordinatentupel der Mittelpunkte sich nicht überlappender Kugeln um. Wenn die Kugeln einen Radius
von dem gerade betrachteten Wort, so dass eine Korrektur möglich ist. In den Fehlerkorrekturcodes, die auf Kugelpackungen beruhen, wandelt man die Verschlüsselungszeichen in Koordinatentupel der Mittelpunkte sich nicht überlappender Kugeln um. Wenn die Kugeln einen Radius ![]() haben, dann lassen sich weniger als
haben, dann lassen sich weniger als ![]() Fehler korrigieren.
Fehler korrigieren.
4.5. Weitere Fragen…
Es liegt nun an Ihnen, weitere Fragen zu stellen. Wie Sie bereits gesehen haben, gibt es viele einfache Fragen mit wichtigen Anwendungen und deren tiefgehende Beantwortungen wurden in den angesehensten wissenschaftlichen Zeitschriften, wie z.B. Nature, Science und Annals of Mathematics, veröffentlicht.
5. Die Gültigkeit computergestützter Beweise
Der Beweis, dass eine optimale Kreispackung im zweidimensionalen Fall eine Dichte von ![]() hat, zeigt, dass es möglich ist, strenge Beweise anzugeben, wenn unendlich viele Fälle zu analysieren sind. Diesen Beweis kann noch jeder nachvollziehen, aber beim Beweis, dass gilt:
hat, zeigt, dass es möglich ist, strenge Beweise anzugeben, wenn unendlich viele Fälle zu analysieren sind. Diesen Beweis kann noch jeder nachvollziehen, aber beim Beweis, dass gilt: ![]() ist das schwierig. Hier gilt es
ist das schwierig. Hier gilt es ![]() Fälle zu analysieren, und jeder Fall ist so komplex, dass dazu ein Computer notwendig ist – etwa
Fälle zu analysieren, und jeder Fall ist so komplex, dass dazu ein Computer notwendig ist – etwa ![]() Gigabyte umfassen die Programme. Die Programme sind jedermann zugänglich. Die Programmierung dauerte einige Jahre. Wer also hat die Zeit und die Fähigkeit, um alle die Details zu überprüfen? Sicher gibt es Strategien, um Fehler zu minimieren, und Hales und Solomon haben einige von diesen auch benutzt. Z.B. schrieben die beiden Autoren das Programm parallel und unabhängig voneinander. Das Programm könnte auf verschiedenen Computern mit verschiedenen Compilern und Prozessoren gleichzeitig laufen. Die Unterprogramme könnten bekannte Softwarepakete verwenden, die über Jahre hinweg getestet wurden, usw.
Gigabyte umfassen die Programme. Die Programme sind jedermann zugänglich. Die Programmierung dauerte einige Jahre. Wer also hat die Zeit und die Fähigkeit, um alle die Details zu überprüfen? Sicher gibt es Strategien, um Fehler zu minimieren, und Hales und Solomon haben einige von diesen auch benutzt. Z.B. schrieben die beiden Autoren das Programm parallel und unabhängig voneinander. Das Programm könnte auf verschiedenen Computern mit verschiedenen Compilern und Prozessoren gleichzeitig laufen. Die Unterprogramme könnten bekannte Softwarepakete verwenden, die über Jahre hinweg getestet wurden, usw.
Aber selbst dann bleiben solche Beweise umstritten, und es bedarf eines langen Entscheidungsprozesses, bis wissenschaftliche Gremien einen solchen Beweis akzeptieren. In dem Fall der Kepler-Vermutung erschien der (gekürzte) Beweis 2005 endlich in „Annals and Mathematics“, eine der angesehensten mathematischen Zeitschriften. Aber die mathematische Community sucht immer noch nach einem stärker „mathematischen“ Beweis. Parallel dazu suchten Mathematiker und Wissenschaftler in der theoretischen Informatik nach formalen Beweisen, d.h. nach Beweisen, in denen jeder logische Schritt von einem Computer überprüft werden kann. So ist es z.B. der Zweck des Flyspeck-Projektes, einen formalen Beweis der Kepler-Vermutung zu finden.
http://code.google.com/p/flyspeck/wiki/FlyspeckFactSheet
Der erste Satz, der computerunterstützt bewiesen wurde, war der Vier-Farben- Satz. Er zeigt, dass vier Farben ausreichen, um jede Karte einzufärben, so dass zwei benachbarte Gebiete nicht die gleiche Farbe haben. Dies wurde 1976 von Kenneth Appel und Wolfgang Haken bewiesen. Zu dieser Zeit hätte „Annals of Mathematics“ einen computerunterstützten Beweis nicht akzeptiert. Die Zeiten haben sich geändert und der Computer hat die Methoden der Mathematik revolutioniert.
Literatur
[1] A. Donev, I. Cisse, D. Sachs, E. Variano, F. H. Stillinger, R. Connelly, S. Tarquato and P.M. Chikin, Improving the density of jammed disordered packings using ellipsoids, Science, 303 (2004), 990–993.
[2] T. Hales, Cannonballs and honeycombs, Notices of the American Mathematical Society, 47 (2000), 440–449.
[3] C. Song, P. Wang and H.A. Maske, A phase diagram for jammed matter, Nature, 453 (2008), 629–-632.
[4] G.C. Szpiro, Kepler’s conjecture, John Wiley & Sons, Inc., 2003.
Anmerkung: Der Artikel wurde von Herbert Glaser, Christin Landeck und Hans-Georg Weigand (Universität Würzburg – www.dmuw.de) vom Englischen ins Deutsche übersetzt.
Weitere Klein-Artikel in anderen Sprachen verfügbar: Englisch, Französisch, …
Andere Sprachen: Englisch, Französisch, Italienisch, Spanisch, Arabisch, Khmer

 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português