Originating author is Christiane Rousseau.
Mathematics offers tools for classifying objects. But is that of any practical use? More than we can imagine at first sight… It could allow us to conclude that a knot cannot be unknotted without cutting the rope, regardless how you move it in space. It could also tell you that you wrongly assembled your Rubik’s cube after dismantling it into pieces, and that there is no use trying to solve it.
In practice, classifying objects means grouping objects in classes of objects sharing some common properties. One very efficient way to do this is through an equivalence relation. Then, each object belongs to an equivalence class. But, this does not mean that we have an efficient way of describing an equivalence class! The mathematical notion of invariant offers an efficient way to do this. An invariant is some mathematical object (it could be simply a number) that is the same for all members of an equivalence class. Among the invariants we distinguish the complete invariants that characterize an equivalence class.
In this vignette, we will mostly work with examples and see how the notion of invariant is widely spread among mathematics, especially algebra and geometry. You will then be able to add your own examples.
The minimum number of crossings of a knot.
What we call in mathematics a knot is simply a closed curve in space (see Figure 1).

Figure 1: Three knots in space. The minimum number of crossings of the trefoil is 3, and that of the figure eight knot is 4.
It is the tradition to represent it by a planar drawing with crossings where we could see which parts are above and which parts are below as in Figures 2 and 3.
On Figure 2 (a) you see the trivial knot with no crossing. Of course, if the knot were a rope, then we could move it in space and draw different presentations with more crossings as in (b) and (c).
Figure 3 presents the left trefoil knot with three crossings. It is not possible to present this knot with less than three crossings: proving this is not trivial, but we will skip this here. There are different ways of representing a knot. Indeed, Figure 3 (a) and (c) are two presentations of the same knot.
So far, we have not defined the equivalence relation on knots, although we have used it implicitly. The one we will use is that two knots are equivalent if one can be transformed into the other through moving the knot in space and stretching it or compressing it. With that equivalence relation, the minimal number of crossings of a knot is an invariant. There are two equivalence classes of knots, for which the minimal number of crossings is ![]() : the left trefoil and right trefoil in Figure 3 are not equivalent: again a formal proof of this result is not trivial (by lopez). This means that the minimal number of crossings is not sufficient to classify knots under our equivalence relation. This brings us to the definition of complete invariant.
: the left trefoil and right trefoil in Figure 3 are not equivalent: again a formal proof of this result is not trivial (by lopez). This means that the minimal number of crossings is not sufficient to classify knots under our equivalence relation. This brings us to the definition of complete invariant.
An invariant is complete is two objects are equivalent if and only if they have the same complete invariant. The minimal number of crossings of a knot is not a complete invariant since the left and right trefoils are not equivalent, although they both have a minimal number of crossings of ![]() . But it allows us to decide that the trefoil is not equivalent to the trivial knot.
. But it allows us to decide that the trefoil is not equivalent to the trivial knot.
As a general rule, if two objects do not have the same invariant(s), then they are not equivalent.
The eccentricity of a conic.
Let us revisit the not so standard definition of a conic with a focus and a directrix. Given a point ![]() , a line
, a line ![]() not passing through
not passing through ![]() , and a positive number
, and a positive number ![]() , the conic with focus
, the conic with focus ![]() , directrix
, directrix ![]() and eccentricity
and eccentricity ![]() is the geometric locus of points, whose ratio of distances to
is the geometric locus of points, whose ratio of distances to ![]() and
and ![]() is equal to
is equal to ![]() . More precisely, if
. More precisely, if ![]() is a point on the plane and if
is a point on the plane and if ![]() is the projection of
is the projection of ![]() on
on ![]() , then
, then ![]() is on the conic if and only if (see Figure 5)
is on the conic if and only if (see Figure 5)
The eccentricity is a description of the shape of the conic (see Figure 4). It is an invariant under an equivalence relation which preserves shape. What could be such an equivalence relation? This equivalence relation is the similarity. A similarity is an affine transformation which preserves angles. Using complex numbers notation, it can be of the form ![]() , if it preserves orientation or
, if it preserves orientation or ![]() if it reverses orientation. Two geometric objects in the plane are similar if one is the image of the other under a similarity.
if it reverses orientation. Two geometric objects in the plane are similar if one is the image of the other under a similarity.
What is remarkable with this definition of a conic through (1) is that it gives a one line proof that two conics are similar if and only if they have the same eccentricity. Indeed, a similarity preserves lines, ratios of distances and orthogonal projections. Hence, the set of points satisfying (1) is sent by a similarity to the set of points ![]() satisfying
satisfying ![]() , where
, where ![]() is the image of
is the image of ![]() , and
, and ![]() is the projection of
is the projection of ![]() on the image
on the image ![]() of
of ![]() . As a particular case, we get that all parabolas are similar.
. As a particular case, we get that all parabolas are similar.
The dimension of a topological space.
A topological space is roughly a geometric object formed by a set of points equipped with a set of neighborhoods of each point. Then, points in a neighborhood of a point ![]() are close to the point
are close to the point ![]() . Also a continuous function between topological spaces sends close points to close points. We want to define a notion of equivalence between topological spaces which would formalize the following: suppose the topological space is made of some elastic material that we can deform, expand or compress. Then, as long as we do not tear the material, we would like to say that the initial space and the final space are equivalent. The equivalence relation reflecting this is the notion of homeomorphic topological spaces.
. Also a continuous function between topological spaces sends close points to close points. We want to define a notion of equivalence between topological spaces which would formalize the following: suppose the topological space is made of some elastic material that we can deform, expand or compress. Then, as long as we do not tear the material, we would like to say that the initial space and the final space are equivalent. The equivalence relation reflecting this is the notion of homeomorphic topological spaces.
Two topological spaces ![]() and
and ![]() are homeomorphic if there exists a bijection
are homeomorphic if there exists a bijection ![]() , which is continuous, and the inverse of which is continuous. We then say that the map
, which is continuous, and the inverse of which is continuous. We then say that the map ![]() is a homeomorphism between
is a homeomorphism between ![]() and
and ![]() .
.
It is then possible to define the notion of dimension of a topological space. How to define the dimension of a topological space is subtle, and we will not go into the details here. In the particular case where the topological space is a subset of ![]() , we refer to the vignette Dimension. For your intuition, a curve is a
, we refer to the vignette Dimension. For your intuition, a curve is a ![]() -dimensional object, a surface, a
-dimensional object, a surface, a ![]() -dimensional object, and a volume a
-dimensional object, and a volume a ![]() -dimensional object. So a sphere has dimension
-dimensional object. So a sphere has dimension ![]() , and the filled ball dimension
, and the filled ball dimension ![]() . What is important is that the dimension of a topological space is an invariant for the equivalence relation we just defined. A line is not homeomorphic to a plane.
. What is important is that the dimension of a topological space is an invariant for the equivalence relation we just defined. A line is not homeomorphic to a plane.
Dimension is not a complete invariant since, for instance, the line and the circle both have dimension 1, but are not equivalent.
The genus of a surface.
We now consider surfaces, and we limit ourselves to bounded closed surfaces. Examples are given in Figure 6.
These surfaces have a tangent plane at each point: we say that they are differentiable and they are orientable, which means that they have two sides: the interior and the exterior. We want to define an equivalence between differentiable surfaces: two differentiable surfaces ![]() and
and ![]() are diffeomorphic if there exists a bijection
are diffeomorphic if there exists a bijection ![]() which is differentiable (although we do not say how we define differentiability of a map between two surfaces). It turns out that two differentiable surfaces are diffeomorphic if and only if they are homeomorphic.
which is differentiable (although we do not say how we define differentiability of a map between two surfaces). It turns out that two differentiable surfaces are diffeomorphic if and only if they are homeomorphic.
A complete invariant can be defined in that case: the genus of the surface. Let’s look again at the surfaces appearing in Figure 6: each of these surfaces is homeomorphic to a sphere with some handles: ![]() handle for the sphere, one handle for the torus (donut), two handles for the
handle for the sphere, one handle for the torus (donut), two handles for the ![]() -torus, etc. The genus is simply the number of handles. Saying that the genus is a complete invariant is very deep: it amounts to saying that any bounded closed orientable surface is diffeomorphic to a sphere with
-torus, etc. The genus is simply the number of handles. Saying that the genus is a complete invariant is very deep: it amounts to saying that any bounded closed orientable surface is diffeomorphic to a sphere with ![]() handles or, equivalently, to an
handles or, equivalently, to an ![]() -torus.
-torus.
For those of you who may have seen the Euler characteristic ![]() of a surface, the genus is nothing else than
of a surface, the genus is nothing else than ![]() . Hence, the Euler characteristic is also a complete invariant.
. Hence, the Euler characteristic is also a complete invariant.
The Jordan normal form of a matrix.
We give this example for those of you who remember the Jordan normal form of a matrix. Otherwise, you may just skip this example, since the Jordan normal form of a matrix is too long and technical to be recalled here. When we consider a linear map ![]() , it is represented in the canonical basis by an
, it is represented in the canonical basis by an ![]() matrix
matrix ![]() . If we now change to a new basis, then the matrix
. If we now change to a new basis, then the matrix ![]() is changed to a matrix
is changed to a matrix ![]() , where
, where ![]() is the transition matrix from the canonical basis to the new basis.
is the transition matrix from the canonical basis to the new basis.
A natural equivalence relation on matrices is that of similarity. Two matrices ![]() and
and ![]() are similar if and only if there exists an invertible matrix
are similar if and only if there exists an invertible matrix ![]() such that
such that ![]() . That amounts to say that these two matrices represent the same linear map in two different bases.
. That amounts to say that these two matrices represent the same linear map in two different bases.
A complete invariant under the relation of similarity is the Jordan normal form of the matrix. Two matrices are similar if and only if they have the same Jordan normal form, up to a permutation of the Jordan blocks. It is worth remarking here that the complete invariant is just a distinguished element of the equivalence class.
The sign of a permutation.
We consider here permutations of ![]() elements and we classify them as even and odd permutations.
elements and we classify them as even and odd permutations.
A transposition is a permutation of two elements of the set. Any permutation is a composition of a finite number of transpositions. The choice of transpositions in this decomposition is not unique, but the parity of the number of transpositions used in the decomposition is always the same, allowing to define without ambiguity what is an even permutation and what is an odd permutation. Two permutations are equivalent if and only if the second one is the composition of the first one with an even permutation. The parity of a permutation is an invariant under this equivalence relation.
The classification of friezes.
A frieze is an infinite ribbon decorated with a pattern that is repeated periodically as in Figure 7. We call a symmetry of the frieze, a geometric transformation which sends the frieze to the frieze: we say that the frieze is invariant under this transformation. All the friezes are invariant under an infinite number of translations, which are all compositions of a minimal translation ![]() of length
of length ![]() , or its inverse
, or its inverse ![]() . Look at Figure 7: these translations are the only symmetries of the first frieze, while the other friezes have additional symmetries. For instance, the second is symmetric under vertical reflections, and the third under a horizontal reflection with respect to the middle line of the frieze.
. Look at Figure 7: these translations are the only symmetries of the first frieze, while the other friezes have additional symmetries. For instance, the second is symmetric under vertical reflections, and the third under a horizontal reflection with respect to the middle line of the frieze.
Two friezes are equivalent if they have the same group of symmetries. It is a deep theorem that there are exactly seven equivalence classes, which are represented in Figure 7. Instead of listing all symmetries of a frieze, it is more elegant to list generators for the symmetries: there are only a finite number of them, and all symmetries are obtained by composition of a finite number of generators or their inverse. Here are lists of generators for the seven classes
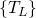 ;
;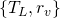 , where
, where 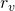 is a reflection with respect to a vertical axis;
is a reflection with respect to a vertical axis;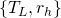 , where
, where 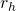 is the horizontal reflection with respect to the middle line;
is the horizontal reflection with respect to the middle line;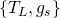 , where the glided symmetry,
, where the glided symmetry, 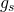 , is the composition
, is the composition 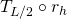 ;
;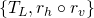 , where
, where 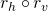 is the rotation of angle
is the rotation of angle 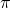 ;
;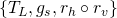 ;
;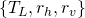 .
.
The same kind of classification can be done for the tiling of the planes: a tiling of the plane is invariant under two translations in non collinear directions. There are ![]() equivalence classes called crystallographic groups because of the applications in crystallography. The same problem can be considered in three dimensions with patters invariant under three translations in three linearly independent directions: in this case there are
equivalence classes called crystallographic groups because of the applications in crystallography. The same problem can be considered in three dimensions with patters invariant under three translations in three linearly independent directions: in this case there are ![]() equivalence classes. These classifications have important applications in crystallography. Usually, chemical substances in a given equivalence class share common chemical properties.
equivalence classes. These classifications have important applications in crystallography. Usually, chemical substances in a given equivalence class share common chemical properties.
The Rubik’s cube.
Mathematics provides an algorithm to solve the Rubik’s cube (Figure 8).
If the cube is fixed in space, then there are twelve elementary movements that can be done: all of these are of the form: rotation of one fourth of a turn of one face: front face, back face, top face, bottom face, left face, right face. Since there are six faces and rotations can be in two different directions, this gives the twelve movements.
Now you are worried: your friend dismantled the cube into its pieces and they all have been mixed. You have put tog the together the cube, but you are playing with it for hours and you do not succeed to have all faces the same color. Is it possible that you wrongly assembled the cube?
This leads us to introduce an equivalence relation on the configurations of the Rubik’s cube: a configuration of the cube is any way of assembling the pieces of the cube. Two configurations are equivalent if and only if we can transform one to the other by a sequence of elementary movements.
It turns out that there exists a complete invariant for this equivalence relation. Hence, you know how to answer your question! It suffices that you check if the present position of your cube has the same complete invariant as the configuration of the cube with faces of the same color. Exactly one configuration out of ![]() is allowed. So you had 11 chances out of 12 of having wrongly reassembled the cube.
is allowed. So you had 11 chances out of 12 of having wrongly reassembled the cube.
The description of the invariant is a bit technical. Note that the elementary movements induce a permutation of the corner blocks and a permutation of the side blocks. Some relation must be satisfied between these two permutations for the configuration to be allowed.
We now describe the invariant. You may decide to stop here and go directly to the conclusion.
The Rubik’s cube has ![]() cubes in the corners and
cubes in the corners and ![]() in the middle of the sides. A position is given by
in the middle of the sides. A position is given by
- a permutation
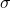 of the corner blocks;
of the corner blocks; - a permutation
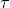 of the side blocks;
of the side blocks; - a rotation of
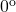 ,
, 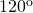 or
or 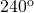 on each corner, which can be viewed as a composition of
on each corner, which can be viewed as a composition of 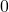 ,
,  or
or 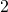 rotations of
rotations of 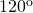 ;
; - a rotation of
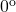 or
or 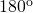 on each side which can be viewed as a composition of
on each side which can be viewed as a composition of 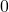 or
or  rotations of
rotations of 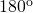 .
.
The first part of the invariant is the difference between the signature of ![]() and the signature of
and the signature of ![]() , modulo
, modulo ![]() , which we call
, which we call ![]() .
.
How to measure the rotation of the corners or sides? This is done in a non canonical way. On the initial cube we mark one external face of each corner (among ![]() such faces) and one face of each side (among two faces) as, for instance, in Figure 9 (a).
such faces) and one face of each side (among two faces) as, for instance, in Figure 9 (a).

Figure 9: The corners of the Rubik’s cube have been marked with dark green stars and the sides stars with black stars. In (b), we see another configuration after we have made one rotation of the blue face.
We want to compute the invariant on another configuration (for instance Figure 9 (b)). Once we have moved the cube, it may happen that the marked face of a corner is not at the place of the marked face for the solved Rubik’s cube. We count the number of rotations of ![]() around an axis directed from the corner to the center of the cube to bring it to the adequate place.
around an axis directed from the corner to the center of the cube to bring it to the adequate place.
We do this for all corners and we take the sum of the numbers of rotations, The second part of the invariant is this sum, reduced modulo ![]() , which we call
, which we call ![]() . In Figure 9 (b), for two corners, we need to make one rotation, and for two other corners, we need to make two rotations, while we do not move the four other corners. The sum adds to six. Hence,
. In Figure 9 (b), for two corners, we need to make one rotation, and for two other corners, we need to make two rotations, while we do not move the four other corners. The sum adds to six. Hence, ![]() for Figure 9 (b).
for Figure 9 (b).
We do the same for the sides. We count the number of rotations of ![]() around an axis pointed towards the center of the cube to bring it to the adequate place.
around an axis pointed towards the center of the cube to bring it to the adequate place.
We do this for all sides, and add up the numbers of rotations. The third part of the invariant is this sum, reduced modulo ![]() , which we call
, which we call ![]() . In Figure 9 (b), no side rotations are needed, yielding
. In Figure 9 (b), no side rotations are needed, yielding ![]() .
.
The invariant is the triplet ![]() . You may argue that the number of rotations we count for each corner (or side) is completely subjective: it depends on the special face we have marked. You are right! But, what we consider is the sum of these numbers for all corners. You can make tests by changing one marked face and check that the sum remains the same!
. You may argue that the number of rotations we count for each corner (or side) is completely subjective: it depends on the special face we have marked. You are right! But, what we consider is the sum of these numbers for all corners. You can make tests by changing one marked face and check that the sum remains the same!
It is easy to verify that, for the solved Rubik’s cube, the invariant is ![]() . It turns out that the triplet
. It turns out that the triplet ![]() is a complete invariant. This means in particular that, given an initial configuration of the cube, it is possible to solve the cube if and only if the invariant is
is a complete invariant. This means in particular that, given an initial configuration of the cube, it is possible to solve the cube if and only if the invariant is ![]() .
.
Then, how do you assemble the cube from its pieces? You can put the first seven corner blocks at random. When you place the eighth one, make sure to choose its orientation so that ![]() (one chance among three). Then, you start placing the twelve side blocks. You can place the first ten ones at random. When you come to the 11th position you must choose the right side block among the remaining two so that
(one chance among three). Then, you start placing the twelve side blocks. You can place the first ten ones at random. When you come to the 11th position you must choose the right side block among the remaining two so that ![]() (one chance among two). You have then one remaining side block for the
(one chance among two). You have then one remaining side block for the ![]() -th position. Make sure to choose its orientation so that
-th position. Make sure to choose its orientation so that ![]() (one chance among two).
(one chance among two).
Conclusion.
Classifying objects is a fundamental problem in mathematics and in science in general. Invariants are very powerful tools in these problems. We have illustrated this with several examples. Most likely, you will encounter many more in your explorations of mathematics and you can start building your own collection with your favorite ones.







