Von Graeme Cohen.
Von allen bekannten Funktionen, wie zum Beispiel den Winkel-, Exponential- oder Logarithmusfunktionen, sind sicherlich die Funktionswerte von Polynomfunktionen am leichtesten zu berechnen. Dieser Artikel soll erstens den Begriff der Potenzreihe einführen, die auch als Polynomfunktion unendlichen Grades verstanden werden kann, und zweitens zeigen, wie mit ihrer Hilfe Funktionswerte von Funktionen mit einem Taschenrechner berechnet werden können. Wenn ein Taschenrechner Werte von trigonometrischen, exponentiellen oder logarithmischen Funktionen berechnen soll, so erreicht man dieses, indem die Funktionswerte von Polynomfunktionen berechnet werden, die man für solche Potenzreihen erhält, die für jene Funktionen repräsentativ sind und ausreichend gute Näherungen darstellen. Dies ist zwar der direkte Weg, aber es gibt oft bessere Möglichkeiten. Wir werden hier insbesondere eine Potenzreihe für die Funktion $\sin x$ herleiten und darlegen, wie man den direkten Ansatz verändern kann, um ihre Werte besser zu approximieren. Dabei werden wir auf Tschebyschow-Polynome zurückgreifen, die in vielerlei Hinsicht für einen ähnlichen Zweck und in vielen weiteren Anwendungen verwendet werden. (Für trigonometrische Funktionen ist der CORDIC-Algorithmus oft die bevorzugte Auswertungsmethode – ein Thema, das sich vielleicht für einen weiteren Klein-Artikel anbieten würde.)
Im Sinne von Felix Klein greifen wir hier auf einen grafischen Ansatz zurück. Ansonsten verwenden wir nur grundlegende Kenntnisse und Techniken aus Trigonometrie und Analysis.
Manipulationen mit Hilfe der geometrischen Reihe
Die geometrische Reihe $1+x+x^2+x^3+\cdots $ ist die einfachste Potenzreihe. Die Summe dieser Reihe existiert für $|x|< 1$. Es gilt
$$1+x+x^2+x^3+\cdots=\frac 1{1-x}, \quad \mbox{wenn}\ |x|<1. \qquad\qquad (1)$$
Die allgemeine Form einer Potenzreihe ist
$$a_0+a_1x+a_2x^2+a_3x^3+\cdots,$$
also handelt es sich bei der obigen geometrischen Reihe um eine Potenzreihe, in der alle Koeffizienten $a_0,\,a_1,\,a_2,\,\ldots$ gleich $1$. sind. Da in diesem Fall die Reihe für $|x|< 1$ gegen $1/(1-x)\,$ konvergiert, sagt man, die Funktion $f$ mit
$$f(x)=\frac1{1-x}, \quad |x|< 1,$$
hat die Reihenentwicklung $1+x+x^2+x^3+\cdots$ oder $f$ wird durch diese Reihe dargestellt. Wir interessieren uns zunächst für weitere Funktionen, die sich durch Potenzreihen darstellen lassen.
Viele dieser Funktionen erhält man direkt aus dem Ergebnis in (1). Zum Beispiel ergibt das Ersetzen von $x$ durch $-x^2$ sofort eine Reihendarstellung der Funktion $1/(1+x^2)$ wobei $|x|< 1$,:
$$1-x^2+x^4-x^6+\cdots=\frac 1{1+x^2}, \quad \mbox{wenn}\ |x|<1. \qquad\qquad (2)$$
Leiten wir beide Seiten der Gleichung (1) ab, so erhalten wir eine Reihendarstellung der Funktion $1/(1-x)^2$:
$$1+2x+3x^2+4x^3+\cdots=\frac 1{(1-x)^2}, \quad \mbox{wenn}\ |x|< 1.$$
Wir können auch beide Seiten von (1) integrieren. Dazu multiplizieren wir sie zunächst mit $-1$ schreiben dann $t$ anstatt $x$ und integrieren nach $t$ von $0$ bis $x$, wobei $|x|< 1$:
$$-\int_0^x (1+t+t^2+t^3+\cdots)\,dt=-\int_0^x\frac {dt}{1-t}$$
und damit
$$-x-\frac{x^2}2-\frac{x^3}3-\frac{x^4}4-\cdots=\log\,(1-x), \quad \mbox{wenn}\ |x|< 1.$$
Auf diese Weise erhalten wir also eine Reihendarstellung der Funktion $\log\,(1-x)$ für $|x|< 1$. Genauso ergibt sich aus (2)
$$x-\frac{x^3}3+\frac{x^5}5-\frac{x^7}7+\cdots=\tan^{-1}x, \quad \mbox{wenn}\ |x|< 1. \qquad\qquad (3)$$
Vieles von dem, was wir hier gezeigt haben (und später noch zeigen werden), verlangt nach Beweisen, aber diese wollen wir den Fachbüchern überlassen.
Die Potenzreihe der Sinusfunktion
Als Nächstes werden wir zeigen, wie man eine Potenzreihendarstellung für $\sin x$ findet. Generell können wir die Sinusfunktion als Potenzreihe auf folgende Weise schreiben:
$$\sin x=a_0+a_1x+a_2x^2+a_3x^3+\cdots. \qquad\qquad (4)$$
Setzt man $x=0$ so ist $a_0=0$. Beidseitiges Differenzieren von (4) ergibt
$$\cos x=a_1+2a_2x+3a_3x^2+4a_4x^3+\cdots.$$
Setzt man wieder $x=0$, so erhält man $a_1=1$. Nun fährt man fort, beide Seiten zu differenzieren und $x=0$ zu setzen:
$$-\sin\,x = 2a_2+3\cdot2a_3x+4\cdot3a_4x^2+5\cdot4a_5x^3+\cdots, \qquad\mbox{so}\ a_2=0,$$
$$-\cos\,x = 3\cdot2a_3+4\cdot3\cdot2a_4x+5\cdot4\cdot3a_5x^2+6\cdot5\cdot4a_6x^3+\cdots, \mbox{ so } a_3=\frac{-1}{3\cdot2}=\frac{-1}{3!},$$
$$\sin\,x = 4\cdot3\cdot2a_4+5\cdot4\cdot3\cdot2a_5x+6\cdot5\cdot4\cdot3a_6x^2+\cdots, \mbox{ so } a_4=0,$$
$$\cos\,x = 5\cdot4\cdot3\cdot2a_5+6\cdot5\cdot4\cdot3\cdot2a_6x+7\cdot6\cdot5\cdot4\cdot3a_7x^2+\cdots, \mbox{ so } a_5=\frac1{5\cdot4\cdot3\cdot2}=\frac1{5!}.$$
Auf diese Weise finden wir eine Formel für alle Koeffizienten $a_0,\,a_1,\,a_2,\,\ldots$, nämlich
$$a_{2n}=0, \qquad\qquad a_{2n+1}=\frac{(-1)^n}{(2n+1)!},$$
für $n=0,\,1,\,2,\,\ldots$. (Die Koeffizienten mit geraden und ungeraden Indizes werden separat angegeben.) Damit gilt
$$\sin\,x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots.$$
Dies ist die Potenzreihendarstellung nach der wir gesucht haben. Ausgehend von der verwendeten Konstruktionsweise können wir davon ausgehen, dass die Reihe $\sin x$ für $x$-Werte in und in der Nähe von $0$ repräsentieren wird (also zum Beispiel für $|x|<1$, wie in den vorherigen Beispielen). Deshalb ist es überraschend, dass man sogar zeigen kann, dass diese Reihe die Funktion $\sin x$ für alle $x$-Werte darstellen kann. Dann sollten Partialsummen der unendlichen Reihe – also Summen die man erhält, wenn man die Summation nach einer endlichen Anzahl von Elementen abbricht – Polynomfunktionen ergeben, die zur Bestimmung von Näherungswerten der Sinusfunktion genutzt werden können, wie sie zum Beispiel in trigonometrischen Wertetabellen oder auf einem Taschenrechner zu finden sind.
Approximation durch Tschebyschow-Polynome
Man schreibe zum Beispiel
$$S_3(x)=x-\frac{x^3}{3!} \quad \mbox{und} \quad S_5(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}.$$
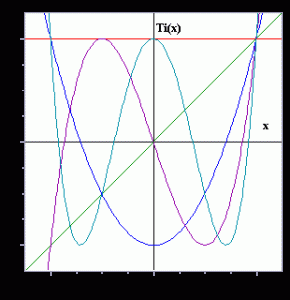
Das kubische Polynom $S_3(x)$ und das Polynom fünften Graden $S_5(x)$ sind – siehe unten – neben $\sin x$ grafisch dargestellt, jeweils im Bereich $-2\le x\le 2$. Man sieht, dass beide sehr gute Approximationen für $-1\le x\le 1$, liefern, jedoch nicht so gute in der Nähe von $x=\pm2$. Das Polynom fünften Grades $S_5$ ist in diesen Außenbereichen wie erwartet viel genauer als das Polynom dritten Grades $S_3$ aber gibt es vielleicht eine bessere Approximation durch eine kubische Polynomfunktion als $S_3$ ?
Für $x=1$ zum Beispiel beträgt der Fehler durch den Gebrauch der kubischen Näherung $\sin1-(1-\frac16)\approx0.0081$. Wir konstruieren nun eine kubische Polynomfunktion $F$ deren Werte sich für $|x|\le1$ von denen von $\sin x$ um weniger als $0.001$ unterscheiden. Die Kurve $y=F(x)$ wurde in den unteren Graphen für $|x|\le2$ eingefügt, und es zeigt sich, dass diese Kurve $y=\sinx$ besser approximiert als $y=S_3(x)$, sogar in der Nähe von $x=\pm2$.

Um $F$ zu konstruieren, werden wir Tschebyschow-Polynome verwenden. Von diesen wird bei Approximationsproblemen oft ausgiebig Gebrauch gemacht, wie wir es auch hier sehen werden. Unter ihnen versteht man die Funktionen $T_k$ mit
$$T_k(x)=\cos k\theta, \quad\mbox{wobei } x = \cos \theta,$$
für ganze Zahlen $k\ge0$ (man kann auch $T_k(x)=\cos\,(k\cos^{-1}\,x)$ schreiben). Wegen der Eigenschaften des Cosinus haben sie alle den Definitionsbereich $[-1,1]$ und ihr Bild liegt ebenfalls in $[-1,1]$. Setzt man $k=0$ und $k=1$ so erhält man
$$T_0(x)=1, \qquad T_1(x)=x,$$
aber es ist nicht sofort offensichtlich, dass die $T_k$ für $k\ge2$ tatsächlich Polynome sind. Um dies einzusehen, rufen wir uns folgende Zusammenhänge in Erinnerung:
$$\cos\,(k+1)\theta=\cos\,(k\theta+\theta)=\cos\,k\theta\,\cos\,\theta-\sin\,k\theta\,\sin\,\theta,$$
und
$$\cos\,(k-1)\theta=\cos\,(k\theta-\theta)=\cos\,k\theta\,\cos\,\theta+\sin\,k\theta\,\sin\,\theta,$$
woraus man durch Addition
$$\cos\,(k+1)\theta=2\cos\,\theta\,\cos\,k\theta-\cos\,(k-1)\theta.$$
erhält.
Damit gilt
$$T_{k+1}(x)=2xT_k(x)-T_{k-1}(x), \quad k\ge1.$$
Setzt man nun $k=1,\,2,\,3,\,\ldots$, so ergibt sich
$$T_2(x) = 2x^2-1, \quad T_3(x) = 4x^3-3x, \qquad\qquad\qquad\quad\ (5)$$
$$T_4(x) = 8x^4-8x^2+1, \quad T_5(x) = 16x^5-20x^3+5x \qquad\qquad (6)$$
und so weiter, wobei man jedes Mal ein Polynom erhält. Da es sich also immer um Polynome handelt, müssen wir ihre Definitionsmengen nicht mehr als auf $[-1,1]$ beschränkt betrachten.
Kehren wir nun zu unserem Ausgangsproblem zurück, $\sin\,x$ für $|x|\le1$ mit einer Abweichung kleiner als $0,001$ zu approximieren. Dabei stellen wir zunächst fest, dass das Polynom fünften Grades $S_5$ diese Eigenschaft besitzt. In der Tat ist
$$\left|\sin1-S_5(1)\right|=\left|\,\sin1-\left(1-\frac16+\frac1{120}\right)\right| < 0.0002 \qquad\qquad (7)$$
und die Theorie der alternierenden unendlichen Reihen zeigt, dass $|\sin\,x-S_5(x)|< 0.0002$ in unserem Intervall gilt, was sicherlich unserer Grafik entspricht. Als Nächstes drücken wir $S_5(x)$ in Form von Tschebyschow-Polynomen aus. Unter Verwendung von (5) und (6) erhalten wir
$$x=T_1(x),$$
$$x^3=\frac14(T_3(x)+3x)=\frac14(T_3(x)+3T_1(x)),$$
$$x^5=\frac1{16}(T_5(x)+20x^3-5x)=\frac1{16}(T_5(x)+5T_3(x)+10T_1(x))$$
und damit
$$S_5(x)=x-\frac{x^3}{6}+\frac{x^5}{120} =T_1(x)-\frac16\cdot\frac14(3T_1(x)+T_3(x))+\frac1{120}\cdot\frac1{16}(10T_1(x)+5T_3(x)+T_5(x))$$
$$=\frac{169}{192}T_1(x)-\frac5{128}T_3(x)+\frac1{1920}T_5(x).$$
Da für $|T_5(x)|\le1$ gilt, dass $|x|\le1$ ist, würde durch Weglassen des Terms $\frac1{1920}T_5(x)$ ein zusätzlicher Fehler von höchstens $\frac1{1920}< 0.0006$ entstehen, der, unter der Verwendung von (7), einen Gesamtfehler kleiner als $0,0008$ ergibt, was immer noch innerhalb unserer Grenze von $0,001$ liegt.
Somit ist
$$\frac{169}{192}T_1(x)-\frac5{128}T_3(x) =\frac{169}{192}x-\frac5{128}(4x^3-3x)=\frac{383}{384}x-\frac5{32}x^3,$$
und die kubische Funktion am Ende ist die Funktion, die wir anfangs mir $F$ bezeichnet haben.
Wir haben also (zum Teil grafisch) gezeigt, dass die Werte der kubischen Funktion
$$F(x)=\frac{383}{384}x-\frac5{32}x^3,$$
für $|x|\le2$ näher an den Werten von $\sin\,x$ liegen als die Werte der kubischen Funktion $x-\frac16x^3$ die man aus der Potenzreihendarstellung von $\sin\,x$ erhält.
Fazit: Der springende Punkt der Geschichte
Die Effektivität der Tschebyschow-Polynome für unsere Zwecke geht auf eine Eigenschaft der Cosinus-Funktion zurück. Diese impliziert, dass für alle ganzen Zahlen $k\ge0$ und für $|x|\le1$ stets $|T_k(x)|\le 1$ gilt. Pafnuti Lwowitsch Tschebyschow, oder in der englischen Literatur oft auch Pafnuty Lvovich Chebyshev, war der russische Mathematiker, der diese Polynome 1854 erstmalverwendete. Sie werden ihm zu Ehren mit $T_k$ bezeichnet.
Das oben beschriebene Verfahren ist als Ökonomisierung von Potenzreihen bekannt und wird in jenem Zweig der Mathematik untersucht, den man Numerische Mathematiknennt. Ökonomisierung ist allerdings nicht immer für eine Bestimmung der Funktionswerte des Sinus-Funktion erforderlich. Da sich $\sin\,x$ näherungsweise wie $x$ verhält, jedenfalls wenn $|x|$ klein ist, reicht diese Abschätzung oft aus! Siehe für weitere Informationen hierzu Chuck Allison, Machine Computation of the Sine Function. Wir erwähnten am Anfang, dass der CORDIC-Algorithmus häufig trigonometrische Funktionen noch besser approximiert, aber für die Auswertung von anderen Funktionen mit einem Taschenrechner, insbesondere der Funktion $\tan^{-1}\,x$, die die langsam konvergierende Potenzreihenentwicklung (3) besitzt, ist Ökonomisierung eine wesentliche Technik.
Vielleicht ist der springende Punkt der Geschichte, dass das Offensichtliche sehr oft noch verbessert werden kann.