Comment Google fonctionne: chaînes de Markov et valeurs propres

Vignette écrite par Christiane Rousseau.
Depuis ses débuts, Google a été “le” moteur de recherche. Ceci est dû à la domination de son algorithme PageRank. En effet, avec l’énorme quantité de pages sur internet, beaucoup de recherches aboutissent à des milliers ou des millions de résultats. Si ceux-ci ne sont pas bien ordonnés, alors la recherche peut n’être d’aucune aide, puisque personne ne peut explorer des millions d’entrées.

Comment l’algorithme PageRank fonctionne-t-il?Nous allons expliquer cela. Mais avant, faisons une recherche sur Google. Le 4 juin 2010, on obtenait 16 300 000 résultats pour Klein project, alors que le projet était juste en train de démarrer. À cette date, la première entrée était

http://www.mathunion.org/icmi/other-activities/klein-project/introduction/
plutôt que

http://www.kleinproject.org/La première URL est l’URL d’une page, qui est située sur le site de l’International Mathematical Union: http://www.mathunion.org. Puisque l’International Mathematical Union est une organisation importante, son site officiel apparaît en premier quand on fait la recherche “International Mathematical Union”. De plus, il communique une part de son importance à toutes ses pages, dont l’une est

http://www.mathunion.org/icmi/other-activities/klein-project/introduction/On peut espérer que quelques mois plus tard la page

http://www.kleinproject.org/
apparaîtra en premier dans une recherche pour Klein project.

Pour expliquer l’algorithme, on modélise le réseau internet par un graphe orienté. Les sommets sont les pages, et les arêtes orientées sont les liens entre les pages. Comme on vient de l’expliquer, chaque page correspond à une URL différente. Par conséquent, un site peut contenir de nombreuses pages. Le modèle ne fait pas de différence entre les pages individuelles d’un site et sa page d’accueil. Mais, logiquement, l’algorithme donnera un meilleur rang à la page d’accueil d’un site important.

Un exemple simple

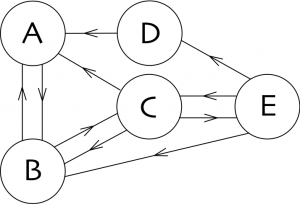
Regardons le réseau simple sur la gauche avec cinq pages nommées $A$ , $B$ , $C$ , $D$ , et $E$ . Ce réseau a quelques liens. Si nous sommes sur la page $A$ , alors il n’y a qu’un lien vers la page $B$ , alors que si nous sommes sur la page $C$ , nous trouvons trois liens, et nous pouvons décider de nous diriger au choix vers la page $A$ , ou $B$ , ou $E$ . Remarquez qu’il y a au moins un lien à partir de chaque page.

Jouons à un jeu, qui est simplement une marche aléatoire sur le graphe orienté. En partant d’une page, à chaque pas on choisit au hasard un lien partant de la page où on se trouve, et on le suit. Par exemple, dans notre graphe, si on part de la page $B$ , alors on peut aller vers $A$ ou $C$ avec la probabilité $1/2$ dans chaque cas, alors que si on part de $D$ , alors on doit nécessairement aller vers $A$ avec la probabilité $1$ . Et on répète le jeu.

Où allons-nous nous trouver après $n$ pas?Pour automatiser le processus, on résume le réseau en la matrice $P$ suivante, où chaque colonne représente la page de départ, et chaque ligne la page d’arrivée.

$P=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix} 0 & \frac12 & \frac13 & 1 & 0 \\ 1 & 0 & \frac13 & 0 & \frac13 \\ 0 & \frac12 & 0 & 0 & \frac13 \\ 0 & 0 & 0 & 0 & \frac13 \\ 0 & 0 & \frac13 & 0 & 0 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}$

Remarquons que la somme des éléments de chaque colonne de $P$ est égale à $1$ et que chaque élément de la matrice est positif ou nul. Les matrices ayant ces deux propriétés sont très spéciales: Chacune de ces matrices est la matrice d’une chaîne de Markov, aussi appelée matrice de transition de la chaîne de Markov. Elles ont toujours $1$ comme valeur propre et il existe un vecteur propre de valeur propre $1$ , dont chaque coordonnée est inférieure ou égale à $1$ et positive ou nulle, et tel que la somme des coordonnées est égale à $1$ . Mais avant de rappeler les définitions de valeur propre et vecteur propre, explorons l’avantage de la représentation matricielle d’un graphe.

Considérons une variable aléatoire $X_n$ à valeurs dans l’ensemble des pages $\{A,B,C,D, E\}$ contenant $N$ pages (ici $N=5$ ). $X_n$ représente la page où nous nous trouvons après $n$ pas de la marche aléatoire. Par conséquent, si on appelle $p_{ij}$ l’élément de la matrice situé à l’intersection de la $i$ -ème ligne et de la $j$ -ème colonne, alors $p_{ij}$ est la probabilité de se trouver sur la page $i$ à l’étape $n+1$ sachant que l’on se trouve sur la page $j$ à l’étape $n$ :

$p_{ij}=\text{Prob}(X_{n+1}= i\mid X_n=j).$

Remarquons que cette probabilité est indépendante de $n$ ! On dit qu’une chaîne de Markov n’a pas de mémoire. Il n’est pas difficile de se rendre compte que les probabilités après deux étapes sont résumées dans la matrice $P^2$ .

Prouvons-le (vous pouvez sauter la preuve si vous préférez). La formule des probabilités totales implique

$\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\text{Prob}(X_{n+2}= i \;\text{et}\; X_{n+1}=k \mid X_n=j).$

Par définition d’une probabilité conditionnelle

$\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\frac{\text{Prob}(X_{n+2}= i \;\text{et}\; X_{n+1}=k \;\text{et}\; X_n=j)} {\text{Prob}(X_n=j)}.$

On utilise une astuce classique: On multiplie et on divise par la même quantité:

$\begin{multline*} \text{Prob}(X_{n+2}=i \mid X_n=j)=\\ \sum_{k=1}^N\frac{\text{Prob}(X_{n+2}= i \;\text{et}\; X_{n+1}=k \;\text{et}\; X_n=j)} {\text{Prob}(X_{n+1}=k \;\text{et}\; X_n=j)}\frac{\text{Prob}(X_{n+1}=k \;\text{et} \; X_n=j)}{\text{Prob}(X_n=j)}. \end{multline*}$

Le premier quotient est égal à

$\text{Prob}(X_{n+2}= i | X_{n+1}=k \;\text{et}\; X_n=j)= \text{Prob}(X_{n+2}= i | X_{n+1}=k ),$

car une chaîne de Markov n’a pas de mémoire au-delà de l’étape précédente. Ainsi,

$\begin{align*}&\text{Prob}(X_{n+2}=i \mid X_n=j)\\ &\qquad\qquad=\sum_{k=1}^N\text{Prob}(X_{n+2}= i \mid X_{n+1}=k)\text{Prob}(X_{n+1}=k\mid X_n=j) \\ &\qquad\qquad=\sum_{k=1}^N p_{ik}p_{kj} \\ &\qquad\qquad=(P^2)_{ij}. \end{align*}$

Dans notre exemple

$P^2=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix}\frac12 & \frac16 & \frac16 & 0 & \frac{11}{18} \\ 0 & \frac23 & \frac49 & 1 & \frac19 \\ \frac12 & 0 & \frac5{18} & 0 & \frac16 \\ 0 & 0 & \frac19 & 0 & 0 \\ 0 & \frac16 & 0 & 0 & \frac19 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}$

Il est clair, par récurrence, que l’élément $(P^m)_{ij}$ de la matrice $P^m$ est la probabilité $\text{Prob}(X_{n+m}=i\mid X_n=j)$ . Il se trouve que

$P^{32} =\begin{matrix} \begin{matrix} \:\:A \quad& \:\:B\quad & \:\:C \quad& \:\:D\quad &\:\: E \quad\end{matrix} & \\ \left(\ \ \begin{matrix} 0.293 & 0.293 & 0.293 & 0.293 & 0.293 \\ 0.390 & 0.390 & 0.390 & 0.390 & 0.390 \\ 0.220 & 0.220 & 0.220 & 0.220 & 0.220 \\ 0.024 & 0.024 & 0.024 & 0.024 & 0.024 \\ 0.073 & 0.073 & 0.073 & 0.073 & 0.073 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix}\end{matrix}$

Toutes les colonnes de $P^{32}$ sont identiques si on choisit d’arrondir les résultats au millème près, de même que les colonnes de $P^n$ pour $n>32$ . Si on choisit de garder une plus grande précision on trouvera aussi une stabilisation des résultats, mais pour $n$ supérieur à $32$ . Par conséquent, après $n$ pas, où $n$ est suffisamment grand, la probabilité d’être sur une page est indépendante du point de départ!

De plus, considérons le vecteur

$\pi^t=(0.293,0.390,0.220,0.024,0.073)$

( $\pi$ est un vecteur-colonne, et son transposé $\pi^t$ est un vecteur-ligne). Il est aisé de vérifier que $P\pi= \pi$ . Si on considère la $i$ -ème coordonnée du vecteur $\pi^t$ comme la probabilité d’être sur la page $i$ à un moment donné $n$ , et donc $\pi^t$ comme la loi de probabilité des pages à l’instant $n$ , alors il s’agit aussi de la loi de probabilité à l’instant $n+1$ . Pour cette raison, le vecteur $\pi$ est appelé la loi stationnaire. Cette loi stationnaire permet d’ordonner les pages. Dans notre exemple, on ordonne les pages de la façon suivante: $B$ , $A$ , $C$ , $E$ , $D$ , et on dit que $B$ est la page la plus importante.

Le cas général

Le cas général peut être traité exactement comme notre exemple. On représente la Toile comme un graphe orienté dans lequel les $N$ sommets représentent les $N$ pages d’internet, et les arêtes orientées représentent les liens entre les pages. On résume le graphe en une matrice $P$ de taille $N\times N$ , où la $j$ -ème colonne représente la $j$ -ème page de départ et la $i$ -ème ligne représente la $i$ -ème page d’arrivée. Dans notre exemple on a trouvé un vecteur $\pi$ tel que $P\pi=\pi$ . Ce vecteur est un vecteur propre de valeur propre $1$ . Rappelons les définitions de valeur propre et vecteur propre.

Définition Soit $P$ une matrice $N\times N$ . Un nombre $\lambda\in \mathbb C$ est une valeur propre de $P$ s’il existe un vecteur non nul $X\in \mathbb C^N$ tel que $PX=\lambda X$ . Un tel vecteur $X$ est appelé un vecteur propre de $P$ de la valeur propre $\lambda$ .

On rappelle également la méthode pour trouver les valeurs propres et vecteurs propres.

Proposition Soit $P$ une matrice $N\times N$ . Les valeurs propres de $P$ sont les racines du polynôme caractéristique, $\det(\lambda I- P)=0$ , où $I$ la matrice identité de taille $N\times N$ . Les vecteurs propres d’une valeur propre $\lambda$ sont les solutions non nulles du système linéaire homogène $(\lambda I - P)X=0$ .

Le théorème suivant, dû à Perron et Frobenius, est très profond et garantit qu’une matrice associée à un graphe admet toujours une solution stationnaire.

Théorème (Théorème de Perron-Frobenius) On considère une matrice de transition d’une chaîne de Markov $P=(p_{ij})$ de taille $N\times N$ (i.e. $p_{ij}\in [0,1]$ pour tout $i,j$ , et la somme des éléments de chaque colonne est égale à $1$ , c’est-à-dire $\sum_{i=1}^Np_{ij}=1$ ). Alors

$\lambda=1$ est une valeur propre de $P$ .
Toute valeur propre $\lambda$ de $P$ vérifie $|\lambda|\leq 1$ .
Il existe un vecteur propre $\pi$ pour la valeur propre $1$ , dont les coordonnées sont toutes positives ou nulles. Sans perdre de généralité, on peut supposer que la somme de ses coordonnées vaut $1$ .

Il est maintenant temps d’admirer la puissance de ce théorème. Pour ce faire, on va supposer plus simplement que la matrice $P$ admet une base de vecteurs propres $\mathcal{B}=\{v_1, \dots , v_n\}$ et on va supposer que $v_1$ est le vecteur $\pi$ du théorème de Perron-Frobenius. Pour chaque $v_i$ , il existe un $\lambda_i$ tel que $Pv_i=\lambda_iv_i$ . Choisissons un vecteur non nul $X$ tel que $X^t= (x_1, \dots, x_N)$ , où $x_i\in[0,1]$ et $\sum_{i=1}^N x_i=1$ . On décompose $X$ dans la base $\mathcal{B}$ :

$X=\sum_{i=1}^N a_iv_i.$

Une preuve technique que l’on omet permet de démontrer que $a_1=1$ . Calculons maintenant $PX$ :

$PX= \sum_{i=1}^Na_i Pv_i= \sum_{i=1}^n a_i\lambda_iv_i,$

puisque $v_i$ est un vecteur propre de la valeur propre $\lambda_i$ . Et si on itère ce procédé on obtient

$P^nX= \sum_{i=1}^n a_i\lambda_i^nv_i.$

Si tous les $\lambda_i$ pour $i > 1$ vérifient $|\lambda < 1|$ alors

$\lim_{n\to \infty} P^nX = a_1v_1=\pi.$

C’est exactement ce qui se passe dans notre exemple!

Remarquons cependant que le théhorème ne garantit pas qu’une matrice $P$ satisfaisant les hypothèses du théorème aura cette propriété. Décrivons les pathologies possibles et le remède.

Les pathologies possibles.

La valeur propre $1$ peut être une racine multiple du polynôme caractéristique $\det(\lambda I -A)=0$ .
La matrice $P$ peut avoir des valeurs propres $\lambda$ autres que $1$ , de modules égaux à $1$ .

Que faire dans ce cas?

Une matrice de transition d’une chaîne de Markov sans pathologies est dite régulière, c’est-à-dire

Définition. Une matrice de transition d’une chaîne de Markov est régulière si

La valeur propre $1$ est une racine simple du polynôme caractéristique $\det(\lambda I -A)=0.$
Toute valeur propre $\lambda$ de $P$ autre que $1$ est de module strictement inférieur $1$ .

Remarquons que la plupart des matrices $P$ sont régulières. Si la matrice de transition d’une chaîne de Markov n’est pas régulière, la stratégie est donc de la déformer légèrement en une matrice régulière.

Remède. On considère la matrice $Q= (q_{ij})$ de taille $N\times N$ , avec $q_{ij} = \frac1N$ pour tout $i,j$ . On remplace la matrice $P$ du réseau par la matrice

(1) $\begin{equation*}P_\beta= (1-\beta) P+ \beta Q, \end{equation*}$

pour un petit $\beta\in [0,1]$ . (La valeur $\beta= 0.15$ a été utilisée par Google). On remarque que la matrice $P_\beta$ a encore des éléments positifs ou nuls et que la somme des éléments de chaque colonne est encore égale à $1$ , donc il s’agit encore d’une matrice de transition d’une chaîne de Markov. Le théorème suivant garantit qu’il existe un petit $\beta$ pour lequel les pathologies disparaissent.

Théorème Étant donnée une matrice de transition d’une chaîne de Markov $P$ , il existe toujours $\beta \geq 0$ , aussi petit que désiré, tel que la matrice $P_\beta$ soit régulière. Soit $\pi$ le vecteur propre $P_\beta$ correspondant à la valeur propre $1$ , normalisé de sorte que la somme de ses coordonnées soit $1$ . Pour la matrice $P_\beta$ , étant donné un vecteur $X$ non nul quelconque, où $X^t= (p_1, \dots, p_N)$ avec $p_i\in[0,1]$ et $\sum_{i=1}^N p_i=1$ , alors

(2) $\begin{equation*}\lim_{n\to \infty} (P_\beta)^nX= \pi.\end{equation*}$

Lien avec le théorème du point fixe de Banach

Une autre vignette (à venir) traite du théorème du point fixe de Banach dont le théorème ci-dessus peut être vu comme un cas particulier. Vous pouvez sauter cette partie si vous n’avez pas lu l’autre vignette. En effet,

Théorème Soit $P$ une matrice de transition d’une chaîne de Markov. On considère $\mathcal{S}=\{X\mid X^t=(p_1, \dots p_N), p_i\in [0,1],\sum_{i=1}^N p_i=1\}$ , avec une distance $d(X,Y)$ adéquate entre les points (cette distance dépend de $P$ ). On considère l’opérateur linéaire $L: \mathcal{S} \rightarrow \mathcal{S}$ défini par $L(X)=PX$ . L’opérateur $L$ est une contraction sur $\mathcal{S}$ , c’est-à-dire qu’il existe $c\in [0,1[$ tel que pour tout $X,Y\in \mathcal{S}$ ,

$d(L(X),L(Y)) \leq c\,d(X,Y).$

Alors il existe un unique vecteur $\pi\in \mathcal{S}$ tel que $L(\pi)=\pi$ .

De plus, étant donné $X_0\in \mathcal{S}$ quelconque, on peut définir la suite $\{X_n\}$ par récurrence, par $X_{n+1} = L(X_n)$ . Alors, $\lim_{n\to \infty} X_n=\pi$ .

Définition de la distance $d$ . La définition de la distance $d$ est un peu subtile et peut être sautée. On l’inclut par souci de complétude pour le lecteur désireux de connaître plus de détails. On se limite au cas où la matrice $P$ est diagonalisable. Soit $\mathcal{B}=\{v_1=\pi, v_2, \dots, v_N\}$ une base de vecteur propres. Les vecteurs $X,Y\in\mathcal{S}$ peuvent être écrits dans la base $\mathcal{B}$ :

$X=\sum_{i=1}^N a_iv_i, \quad Y=\sum_{i=1}^N b_iv_i,$

où $a_i,b_i\in \mathbb C$ . On définit alors

$d(X,Y)=\sum_{i=1}^n |a_i-b_i|.$

Muni cette distance, $\mathcal{S}$ est un espace métrique complet, i.e. toute suite de Cauchy y est convergente.

Ce théorème ne garantit pas seulement l’existence de $\pi$ , mais donne également une méthode pour le construire, comme limite de la suite $\{X_n\}$ . Nous avons vu un exemple de cette convergence dans notre exemple. En effet, la $j$ -ème colonne de $P^n$ est le vecteur $P^n e_j$ , où $e_j^t= (0,\dots, 0, 1, 0, \dots,0)$ est le $j$ -ème vecteur de la base canonique. Bien entendu, dans notre exemple nous aurions pu trouver directement le vecteur $\pi$ en résolvant le système $(I-P)X=0$ avec la matrice

$I-P= \left(\begin{matrix} 1 &- \frac12 & -\frac13 & -1 & 0 \\ -1 & 1 & -\frac13 & 0 & -\frac13 \\ 0 & -\frac12 & 1 & 0 & -\frac13 \\ 0 & 0 & 0 & 1 & -\frac13 \\ 0 & 0 & -\frac13 & 0 & 1 \end{matrix}\right).$

Nous aurions découvert que toutes les solutions sont de la forme $(4s, \frac{16}3s,3s,\frac13 s,s)^t$ avec $s\in\mathbb R$ . La solution dont la somme des coordonnées est $1$ est donc $\pi$ , où

$\pi^t=\left(\frac{12}{41}, \frac{16}{41}, \frac{9}{41}, \frac1{41}, \frac{3}{41}\right).$

Calcul pratique de la loi stationnaire

Nous avons identifié l’idée simple à la base de l’algorithme. Cependant, trouver la loi stationnaire $\pi$ , i.e. un vecteur propre pour la valeur propre $1$ pour la matrice $P_\beta$ dans (1) n’est pas du tout une tâche triviale lorsque la matrice a des millions de lignes et de colonnes: à la fois le temps de calcul et la capacité de mémoire nécessaires à cette réalisation sont de réels défis. La méthode classique du pivot de Gauss n’est d’aucune aide dans ce cas, à cause de la taille du calcul, et parce que la méthode nécessite des divisions par de petits coefficients. Une méthode plus efficace utilise la propriété (2) (voir [LM]). Ceci fait le lien avec la vignette à venir sur le théorème du point fixe de Banach qui montrera que la preuve du théorème fournit un algorithme pour construire le point fixe.

En effet, on commence avec $X_0$ tel que

$X_0^t= (\frac1{N},\frac1{N}, \dots, \frac1{N}),$

et on doit calculer $\lim_{n\to \infty} (P_\beta)^nX_0$ . En général, $P_\beta^nX_0$ pour un nombre $n$ entre $50$ et $100$ donne une approximation suffisamment bonne de $\pi$ . Par récurrence, on calcule $X_{n+1} =P_\beta X_n$ . Même de tels calculs sont assez longs. En effet, de par sa construction, la matrice $P_\beta$ in (1) n’a aucun élément nul. D’un autre coté, la plupart des éléments de la matrice $P$ sont nuls. Donc on doit décomposer le calcul pour profiter de cette propriété, c’est-à-dire

$X_{n+1} = (1-\beta)PX_n +\beta Q X_n.$

À cause de la forme spéciale de $Q$ , il est facile de vérifier que si $X$ est un vecteur dont la somme des coordonnées vaut $1$ , alors $QX= X_0$ . Par conséquent il suffit de calculer la suite

$X_{n+1} = (1-\beta)PX_n +\beta X_0.$

Conclusion

Nous avons présenté la partie publique de l’algorithme PageRank de Google. Vous pouvez déjà expérimenter avec des réseaux simples, et trouver les astuces permettant d’améliorer le rang de votre page personnelle en ajoutant des liens internes et externes de façon optimale. Des parties privées, et plus élaborées, continuent d’être développées. Certaines consistent à remplacer la matrice “neutre” $Q$ de (1) par des matrices reflétant les goûts du promeneur sur la Toile. D’autres assurent que le classement n’est pas trop sensible aux manipulations de ceux essayant d’améliorer le classement de leurs pages.

En conclusion, qu’avons-nous observé? Une idée simple, astucieuse, a mené à une grande percée dans l’efficacité des moteurs de recherche, et à la naissance d’un empire commercial. Même si la mise en œuvre est en elle-même un exploit calculatoire, l’idée originale ne requiert que des mathématiques “élémentaires”, essentiellement de l’algèbre linéaire et des probabilités. Ces outils mathématiques relativement standards, en particulier la diagonalisation de matrices, ont donné leur pleine puissance quand ils ont été utilisés en dehors de leur contexte “normal”. De plus, nous avons mis en lumière les idées unificatrices à l’intérieur de la science, avec le théorème du point fixe de Banach ayant des applications éloignées de son origine.

Bibliographie
[E] M. Eisermann, Comment Google classe les pages webb, http://images.math.cnrs.fr/Comment-Google-classe-les-pages.html, 2009.

[LM] A. N. Langville et C. D. Meyer, A Survey of Eigenvector Methods
for Web Information Retrieval, SIAM Review, Volume 47, Issue 1,
(2005), pp. 135–161.

[RS] C. Rousseau et Y. Saint-Aubin, Mathématiques et
Technologie, SUMAT Series, Springer-Verlag, 2008.

Comment Google fonctionne: chaînes de Markov et valeurs propres

Related

Laisser un commentaire Annuler la réponse

Receive notice of every new vignette.

Search

Meta

Comment Google fonctionne: chaînes de Markov et valeurs propres

Partager :

Related

Laisser un commentaire Annuler la réponse

Receive notice of every new vignette.

Search

Meta