Faire Bewertungen: Das Streben nach Gold

Orginalautoren sind Gabriel Rosenberg und Mark Iwen. (Übersetzt ins Deutsche von Reinhild Kokula, Universität Würzburg)

Es ist nur wenigen Leuten bekannt, dass während der Olympischen Winterspiele 2002 an zwei Teams die Goldmedaille in der Kategorie Paareiskunstlauf verliehen wurde. Diese zwei Medaillen waren das Ergebnis einer umstrittenen Bewertung, die zunächst damit endete, dass die klaren Zuschauerfavoriten kein Gold gewannen. Die Empörung darüber war so groß, dass das Internationale Olympische Komitee (IOK) letztlich eine zweite Goldmedaille an die Zweitplatzierten verleihen musste, um dem Skandal zu begegnen. Eine Folge davon war, dass das System zur Bewertung darüber, welche Eiskunstläufer eine Medaille verdienten, geändert wurde (NB: Vor 2003 bewerteten die Juroren die Teilnehmer individuell und nutzten die Ergebnisse, um die Athleten zu klassifizieren. Diese Klassen (nicht Punkte) wurden dann kombiniert, um insgesamt Preise zu verleihen).

Stellen Sie sich vor, dass Sie Teil des IOK im Jahre 2003 sind und damit beauftragt werden, ein besseres Bewertungssystem zu entwickeln, mit dem Eiskunstlaufwettkämpfe in Zukunft bewertet würden. Welches Bewertungssystem würden Sie für die Einordnung der Eiskunstläufer wählen? Wie würden Sie sichergehen, dass das System fair ist? Wenig überraschend kann die Mathematik diese Fragen beantworten!

Funktionen zur Hilfe: Die Macht der Abstraktion

Ein Weg, über die Erschaffung eines neuen Abstimmungssystems nachzudenken, mit dem man Eiskunstläufer (oder etwas beliebig Anderes) bewertet, ist damit anzufangen, alle möglichen Bewertungssysteme in Betracht zu ziehen. Wir können ein gutes Bewertungssystem konstruieren, indem wir langsam alle möglichen Systeme auf eine kleinere Menge an gewünschten Alternativen einschränken.
Beginnen wir diesen Vorgang, indem wir (eine sehr allgemeine Klasse) alle möglichen Bewertungssysteme modellieren. In dieser Situation wird sich jedes Bewertungssystem letztendlich mit der Rangordnung einer Menge von Eisläufern beschäftigen, basierend auf dem Beitrag von einer Menge an Bewertenden (z.B. den olympischen Juroren). Nehmen wir an, dass unsere Menge der teilnehmenden Eisläufer ist, wobei jeder von ihnen von jedem Juror der folgenden Menge an Juroren bewertet wird:

Jeder Juror weist den Eisläufern eine Bewertung zu, was für jeden Juror eine unterschiedliche Rangordnung der Eisläufer erzeugt. Zum Beispiel könnten die Bewertungen der Juroren für einen bestimmten Wettkampf in den folgenden individuellen Bewertungen resultieren (siehe Tabelle 1).

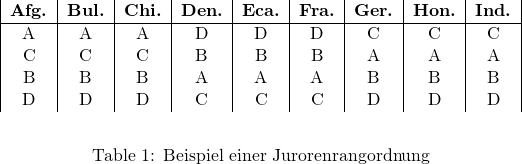
Jedes Bewertungssystem muss diese Menge von neun Individualbewertungen jedes Jurors in eine Endbewertung umwandeln, die den ersten (Gold), zweiten (Silber), dritten (Bronze), vierten, fünften, etc. Platz aus der Menge aller Eisläufer bestimmt, . Mathematisch betrachtet können wir sehen, dass unsere Bewertungssysteme genau die Menge der Funktionen sind, die Ranglisten von als Eingabe nutzen und eine endgültige Bewertung von als Ergebnis erzeugen. Hier repräsentiert die Anzahl der Juroren in .

Einige Eigenschaften eines guten Bewertungssystems

Natürlich können wir erkennen, dass diese Menge von Funktionen zu allgemein ist, um fair zu sein. Zum Beispiel ist die Funktion, die dem zweiten Eisläufer (hier Berezhnaya) unabhängig von der tatsächlichen Bewertung der Juroren eine Goldmedaille zuweist, immer noch ein mögliches Bewertungssystem. Offenkundig müssen wir unsere möglichen Bewertungsfunktionen weiter einschränken, um solche unfairen Bewertungssysteme auszuschließen.

Einstimmige Meinungen respektieren: das Pareto-Optimum

Das Pareto-Optimum ist eine Eigenschaft, die viele Menschen als passend für ein gutes Bewertungssystem ansehen würden. Knapp erklärt sagt das Pareto-Optimum in dem Fall aus, dass ein bestimmter Eisläufer von allen Juroren höher als ein anderer eingeordnet ist, dass ein gutes Bewertungssystem den einstimmig vorgezogenen Eisläufer über einen anderen Eisläufer platziert (z. B.: ist Cohen von allen Juroren höher platziert als Berezhnaya, dann sollte Cohen auf dem Podium besser eingeordnet sein als Berezhnaya). Diese Kondition garantiert im Großen und Ganzen, dass ein Bewertungssystem einstimmige Meinungen respektiert.

Obwohl es schwer ist, ein natürliches Bewertungssystem zu konzipieren, welches zu einem Ergebnis führt, dem alle abgeneigt sind, kann dies tatsächlich passieren, wenn das Bewertungssystem hierarchisch aufgebaut ist. Nehmen Sie also zum Beispiel an, dass unsere vier Eisläufer in folgender Reihenfolge antreten: Asada, Dijkstra, Cohen und dann Berezhnaya. Asada und Dijkstra sind die ersten zwei Eisläufer und nach ihren Auftritten bevorzugen die Juroren Asada mit einer Quote von 6-3. Dann, nachdem Cohen anschließend läuft, stimmen die Juroren mit einer Quote von 6-3 ab, dass Cohen ein besserer Eisläufer als Asada ist. Als Letzter tritt Berezhnaya auf und tatsächlich glauben die Juroren, dass Berezhnaya ein besserer Läufer als Cohen ist mit einer Quote von 6-3. Ein Bewertungssystem, das auf solchen sequenziellen paarweisen Vergleichen basiert, könnte zu der Podiumsplatzierung von Berezhnaya (Gold), Cohen (Silber), Asada (Bronze) und Dijkstra (keine Platzierung) führen. Wenn die Juroren allerdings ihre einzelnen Bevorzugungsranglisten niederschrieben (wie in Tabelle 2, in der jede Spalte die Bewertung eines Juroren wiederspiegelt, vom höchsten Platz oben und dem niedrigsten Platz unten), wären sie schockiert herauszufinden, dass alle von ihnen Dijkstra als besseren Läufer befunden hätten als Berezhnaya. Die Goldmedaille ging an den Eisläufer, der einstimmig schlechter als der Viertplatzierte befunden wurde!

Unabhängigkeit von irrelevanten Alternativen

Bedenken Sie die folgende Situation: Nehmen Sie an, dass Asada und Berezhnaya bereits aufgetreten sind, aber Cohen dies noch vor sich hat. In dieser Situation haben alle Juroren entschieden, welchen der beiden ersten Eisläufer sie bevorzugen, aber sie sind sich noch nicht sicher, wie Cohen im Vergleich sein wird, da er noch nicht aufgetreten ist. Die technischen Helfer, die die Ergebnisse tabulieren, möchten allerdings wissen, wie es zurzeit steht (z.B. vor einer Werbepause). Daher weisen die technischen Helfer die Juroren an, zunächst daraufhin zu bewerten, wie gut sie annehmen, dass Cohen auftreten wird, sodass die Sacharbeiter ankündigen können, wie Asada in Relation zu Berezhnaya platziert werden wird. Die Bewertungsfunktion wird evaluiert und es wird ermittelt, dass Asada vor Berezhnaya auf dem Podium platziert wird. Die Bewertungsfunktion platziert also Cohen irgendwo auf dem Podium, doch jeder weiß, dass diese Rangliste nur eine Mutmaßung ist und sich wahrscheinlich ändern wird, wenn Cohen auftritt.

Später, nach der Werbepause, tritt Cohen auf und manche Juroren ändern ihre Meinung darüber, wie Cohen abschneidet. Allerdings ändern sie nicht ihre Meinung darüber, ob Asada besser als Berezhnaya war, oder umgekehrt. Als die offiziellen Ergebnisse allerdings durch die Bewertungsfunktion tabuliert werden, stellt sich heraus, dass Berezhnaya vor Asada auf dem Podium steht! Das erscheint unfair und ist auch noch schlechtes Fernsehen! Warum sollte die Platzierung Cohens darüber bestimmen, welcher der anderen beiden Eisläufer besser war? Ein System, in dem dieses eigenartige Verhalten nicht auftreten kann, erfüllt die Unabhängigkeit von irrelevanten Alternativen, auch kurz UIA. Im Großen und Ganzen wird ein Bewertungssystem, das UIA erfüllt, vorher etablierte Einzelrangfolgen nicht aufgrund von zukünftigen Auftritten verändern.

Verbesserte Meinungen sollten niemals verletzen: Monotonie

Stellen Sie sich als nächstes eine Situation vor, in der die Medaillenergebnisse wie folgt angekündigt werden: Asada erhält Gold, Berezhnaya erhält Silber und Cohen erhält Bronze. Der bulgarische Juror tritt dann allerdings vor und behauptet, dass seine Stimme falsch verstanden wurde. Diese wurde wie folgt verstanden: Asada, Berezhnaya, Cohen, obwohl er eigentlich Berezhnaya, Asada, Cohen gestimmt hatte. Die Sachbearbeiter berechnen die Ergebnisse neu und kündigen an, dass nun Berezhnaya nur Bronze erhalten solle. Das ist merkwürdig – durch einen Juror höher platziert zu werden, hat Berezhnaya bei der Podiumsplatzierung verletzt! Ein System, in dem eine solche Situation niemals auftreten kann, erfüllt die Monotonie.

Auf den ersten Blick hin erscheint es unlogisch, eine solche Eigenschaft überhaupt zu betrachten. Was für ein Bewertungssystem könnte denn damit enden, dass ein Eisläufer sich benachteiligt fühlt, weil er besser platziert wurde? Erinnern Sie sich allerdings daran, dass ein potentielles Bewertungssystem lediglich eine Funktion ist und es keine Vorgabe existiert, dass sie im Kontext angemessen sein muss.

Es ist allerdings interessant zu vermerken, dass diese sehr vernünftige Eigenschaft von vielen gemeingebräuchlichen Bewertungssystemen NICHT erfüllt wird. So zum Beispiel befriedigt kein System, das eine Folge von Abstimmungen mit Entscheidungslauf ist, die Monotonie – so zum Beispiel auch das Bewertungssystem, dass das IOK nutzt, um die Gastgeberstadt der olympischen Spiele zu bestimmen. Wie oft eine solche nicht-monotone Situation tatsächlich auftritt ist Thema vieler Forschung und Diskussion, doch allein die Tatsache, dass eine solche Situation in einem gegenwärtig genutzten Bewertungssystem möglich ist, kann uns zur Suche nach einem andersartigen Bewertungssystem führen.

Gleichheit: Neutralität und Anonymität

Eine andere Eigenschaft, die wir in unserem Bewertungssystem möglicherweise erwünschen ist die, dass – im Zuge der Fairness – alle Eisläufer gleich behandelt werden. Das bedeutet, dass dieselben Einzelpersonen unabhängig von ihrer Auftrittsreihenfolge, Namen, Nationalität, etc. auftreten sollen. Wir besagen, dass ein System mit dieser Charakteristik die Neutralität erfüllt. Ähnlich möchten wir auch, dass ein Bewertungssystem alle Juroren gleich behandelt. Das bedeutet, dass der Einfluss, den die Stimme eines jeden Jurors auf die letztendliche Rangliste hat, ebenfalls nicht von der Reihenfolge der Bewertung, dem Namen, der Nationalität etc. abhängt. Ein Bewertungssystem, das diese Eigenschaft erfüllt, ist anonym.

Interessanterweise können wir verbreitete (demokratische!) Bewertungssysteme finden, die diese Eigenschaften nicht erfüllen. Zum Beispiel erfüllen Länder, die ihren Anführer basierend auf Stimmenhäufung aus verschiedenen geographischen Bezirken wählen, nicht die Anonymität. Zum Beispiel können in den USA Leute, die in einem Staat mit einer Mehrheit für eine politische Partei leben, ihre Stimme „mehr zählen“ lassen, indem sie temporär in einen anderen Bundesstaat umziehen, in dem die Wahl umkämpfter ist. Das liegt genau daran, dass Wähler aus den „Swing States“ mehr Einfluss darauf haben, welche Kandidaten die Stimmen der Wahlmänner ihres Staates erhalten.

Einige schlechte Nachrichten: Arrow-Theorem

Nun haben wir einige vernünftige Eigenschaften, die unser Bewertungssystem für die Olympischen Spiele erfüllen soll. In diesem Abschnitt werden wir versuchen, eine Menge von guten Bewertungssystem zu orten, die all die oben beschriebenen Eigenschaften erfüllen. Wie oben werden wir ein Panel mit neun Juroren betrachten, die drei Eisläufer bewerten.
Nehmen wir an, dass wir ein neues Bewertungssystem austesten möchten, das angeblich die Konditionen UIA, Monotonie und Neutralität erfüllt. Betrachten wir als Hilfestellung einen Fall, in dem es drei Mengen von Juroren gibt. Nehmen wir an, dass die drei Juroren aus Asien alle die Platzierungsreihenfolge Asada, Berezhnaya, Cohen bevorzugen. Weiterhin nehmen wir an, dass die zwei amerikanischen Juroren die Medaillen in der Reihenfolge Cohen, Asada, Berezhnaya annehmen und zuletzt, dass die vier europäischen Juroren die Reihenfolge Berezhnaya, Cohen, Asada als Rangliste bevorzugen. Unser Bewertungssystem muss eine Reihenfolge für das Podium zurückgeben, aber welche Reihenfolge kann das sein?

Setzen wir unser Beispiel fort und nehmen an, dass unser gutes Bewertungssystem in einer Podiumsreihenfolge resultiert, die Berezhnaya besser platziert als Asada. Weil wir wissen, dass unser System UIA erfüllt, impliziert dies, dass wir mit Berezhnaya vor Asada auf dem Podium enden, wenn die vier europäischen Juroren Berezhnaya vor Asada und die anderen fünf Juroren Asada vor Berezhnaya platzieren (hier wird Cohens Position sich nicht ändern unabhängig davon, wie Berezhnaya relativ zu Asada platziert wird!). Da bekannt ist, dass unser System monoton ist, würde dieses Ergebnis immer noch auftreten, wenn einer der anderen fünf Juroren ebenfalls für Berezhnaya vor Asada gestimmt hat (also verbessert dies Berezhnayas Position nur!). Dies würde bedeuten, dass die vier europäischen Juroren eine diktatorische Macht in dem Sinne haben, dass es garantiert ist, dass Berezhnaya vor Asada platziert wird, WANN AUCH IMMER sie die beiden so platzieren. Da wir angenommen haben, dass unser Bewertungssystem neutral ist, gibt es keine Besonderheit bei Berezhnaya und Asada in diesem Beispiel. WANN AUCH IMMER die europäischen Juroren einen Eisläufer höher als einen anderen platzieren, MÜSSEN die Eisläufer in dieser Reihenfolge auf dem Podium platziert werden. Wenn also die europäischen Juroren als Block abstimmen (sie also alle gleich abstimmen), wird das Podiumsergebnis immer mit ihrer Stimme übereinstimmen, egal wie ein anderer Block gewählt hat. Wir würden dann sagen, dass die europäischen Juroren die diktatorische Macht haben.

Als Ergebnis aus unserer Diskussion aus dem vorherigen Paragraphen können wir argumentieren, dass das obige Profil nicht darin resultieren sollte, dass Berezhnaya vor Asada auf dem Podium platziert wird. Nehmen wir stattdessen an, dass Asada vor Berezhnaya abschließen soll. Dann können wir aber betrachten, wo Cohen in Relation zu Berezhnaya platziert werden soll. Hätte die Podiumsreihenfolge Cohen vor Berezhnaya, so sind wir in einer Situation gelandet, in der die zwei amerikanischen Juroren die einzigen sind, die Cohen vor Berezhnaya platzieren (sodass die Podiumsreihenfolge ihre Meinung wiederspiegelt). Wenn wir nun dieselbe Herangehensweise nutzen wie soeben mit den europäischen Juroren, so würde dies implizieren, dass die amerikanischen Juroren diktatorische Macht haben! Wenn wir nicht möchten, dass eine Minderheit diktatorische Macht hat, sind wir dazu gezwungen, Asada vor Berezhnaya vor Cohen auf dem Podium zu platzieren. Aber das wiederum impliziert, dass Asada vor Cohen abschließt. Bezieht man sich darauf, dass die drei asiatischen Juroren die einzigen waren, die Asada vor Cohen in ihrer Rangfolge vor Cohen platziert haben, würde der Gedankengang mit den europäischen Juroren dazu führen, dass in dieser Situation die asiatischen Juroren eine diktatorische Macht aufweisen. Diktatur ist also unausweichlich!

Da für dieses Profil unser Bewertungssystem zu einer Podiumsreihenfolge führen muss, muss eine der drei Jurorengruppen die diktatorische Macht erhalten. Das bedeutet, dass in jeder Situation, in der diese Gruppe als Block mit den gleichen Reihenfolgen abstimmt, das Podiumsergebnis mit ihrer Abstimmung übereinstimmen wird. Das ist schlimm genug bezüglich der Tatsache, dass wir dann eine Gruppe bestehend aus Minderheiten der Juroren hätten, die bei Zusammenarbeit die Macht hätten, die Ergebnisse des Bewertungssystems zu kontrollieren. Das Problem ist allerdings schlimmer. Sobald wir eine diktatorische Gruppe bestimmt haben, können wir diese Gruppe weiter in zwei Untergruppen einteilen und ähnliche Argumentation wie oben zeigt, dass eine dieser Untergruppen diktatorisch ist. Durch Fortsetzung der weiteren Unterteilung dieser diktatorischen Gruppen erhalten wir letztendlich eine Gruppe bestehend aus einem einzigen Juror – ein Diktator. Kenneth Arrow bewies diese Ergebnisse im Jahre 1950, sogar unter den schwächeren Bedingungen, dass das Bewertungssystem nur die UIA und die Pareto-Kondition erfülle.

Bewertungstheorie

Arrow war einer der Ersten, der Abstimmungen aus dieser mathematischen Perspektive erforschte, also als Funktionen, die bestimmte erwünschte Eigenschaften haben oder nicht haben. Seine Arbeit öffnete allerdings Türen hin zu einem komplett unergründeten Forschungsgebiet, in dem Mathematiker, Ökonomen und Politikwissenschaftler Wege kreuzen und Ideen austauschen darüber, was möglich und was erwünscht ist. Zum Beispiel untersuchten Allan Gibbard im Jahre 1973 und Mark Satterthwaite im Jahr 1975 die Eigenschaft, ob ein Bewertungssystem die (scheinbar unerwünschte) Eigenschaft der Manipulation besitzt. In anderen Worten kann es Situationen geben, in denen jemand ein erwünschtes Ergebnis herbeiführen kann, indem er über seine Prioritäten lügt. Ihre Arbeit führte zu der Schlussfolgerung, dass die einzigen nicht-manipulierbaren Bewertungssysteme einen einzigen Diktator hatten oder sonst mindestens eine Alternative aufwiesen, die nie gewinnen konnte. Forscher haben daraufhin weitere Fragen studiert, so zum Beispiel wie oft eine solche Manipulation möglich ist und wie wahrscheinlich deren Auftreten ist.

Erkenntnis

Wir erkennen, dass mathematische Argumentationen durch sorgfältige, präzise Definitionen und logische Beweise auf in Situationen außerhalb der Mathematik und Naturwissenschaften angewandt werden können. Solche Argumentationen können notwendig sein, um sich von einem Resultat zu überzeugen, das zunächst entgegen der Intuition erscheint. Im Kontext unseres olympischen Beispiels können wir sehen, dass es unmöglich ist, alle vier der guten Charakteristika zu erfüllen, die wir gerne in unserem Bewertungssystem hätten, zumindest wenn es allein auf den Bewertungen der Juroren gestützt ist.

Es gibt allerdings keinen Grund zur Verzweiflung. Unsere obige Analyse zeigt uns, dass wir einfach eine größere Klasse an Bewertungssystemen in unserer Suche nach einem guten System betrachten müssen. Beispiellösungen involvieren die Nutzung der tatsächlichen numerischen Punkte, die jeder olympische Juror für etwas erzeugt, das weiter führt als nur ihre Präferenzen einzuordnen. Andere Fehlerbehebungen binden etwas Zufall in das Bewertungssystem ein. Zum Beispiel könnten wir gelegentlich zufällig die Bewertungen eines beliebigen Jurors vernachlässigen, wodurch wir ein Bewertungssystem etablieren, das nicht von der Form ist, die wir betrachtet haben. Diese letzte Lösung war tatsächlich einer der Aspekte, die als Teil des neuen Bewertungssystems für die Eiskunstlaufwettbewerbe im Jahr 2004 angenommen wurde!

Literatur

For All Practical Purposes by COMAP, 8th ed., W.H. Freeman & Company, 2008.

G. Szpiro, Numbers Rule: The Vexing Mathematics of Democracy, from Plato to the Present, Princeton University Press, 2010.

P. Tannebaum & R. Arnold, Excursions In Modern Mathematics, 7th edition, Prentice Hall, 2009.