 Die Autorin des Originaltexts ist Anna Cannas da Silva.
Die Autorin des Originaltexts ist Anna Cannas da Silva.
Ins Deutsche übersetzt von Katrin Veh und Hans-Georg Weigand (Universität Würzburg)
Symmetrie hat die Menschheit schon immer fasziniert und ist ihr in der Architektur, der Kunst, der Technik und der Wissenschaft von Nutzen gewesen. Seit Tausenden von Jahren wurden symmetrische Muster für die Herstellung von Textilien, Körben, Bodenbelägen, Tapeten, Geschenkpapier und so weiter genutzt. Gegen Ende des 19. Jahrhunderts fand der russische Mathematiker und Mineraloge Yevgraf Fyodorov heraus, dass 17 Symmetrierguppen für Muster in der Ebene existieren [WPG]. Daher können wir beispielsweise genau 17 verschiedene Tapeten hinsichtlich dieser Klassen erhalten und nicht mehr! Bemerkenswert ist auch, dass alle diese Klassen in der Ornamentkunst der Antike gefunden werden können.
Die Existenz dieser 17 Symmetrieklassen wurde in den 1980ern geometrisch bewiesen, indem man Kenntnisse über die Addition von Brüchen und ein wenig Topologie anwendete. Die Erklärung wurde von Bill Thurston entdeckt und von John H. Conway verbreitet. Conway erschuf eine Sprache für Thurstons Ideen hinsichtlich der vier Arten von Symmetrie: Achsensymmetrie, Drehsymmetrie, Verschiebungssymmetrie und Gleitspiegelungssymmetrie, welche wir in Abschnitt 1 kurz beschreiben werden.
| Beachte die Korrektur von Marston Conder am Ende des Artikels. |
Daneben führte Conway eine einprägsame, symbolische Notation ein (![]() , Ziffern,
, Ziffern, ![]() and
and ![]() ). Jede der vier Symmetriearten wird somit von Conway und Thurston mit einer symbolischen Bezeichnung verbunden (Symbole, die den Typ der Symmetrie genau bestimmen), was informativer und angenehmer ist als die alte kristallographische Darstellung.
). Jede der vier Symmetriearten wird somit von Conway und Thurston mit einer symbolischen Bezeichnung verbunden (Symbole, die den Typ der Symmetrie genau bestimmen), was informativer und angenehmer ist als die alte kristallographische Darstellung.
Die Einteilung von Symmetrien in der Ebene im Sinne von Conway und Thurston wird in Abschnitt zwei mithilfe grundlegender Arithmetik besprochen. Die Arbeit endet in Abschnitt drei mit der Untersuchung der Symmetrien einiger portugiesischer Kopfsteinpflaster und der Strandpromenade in Rio de Janeiro (Abbildung 1 Mitte), die vermutlich das bekannteste Beispiel weltweit darstellt.

Abbildung 1: Pflasterungen des Rossio (Lissabon), der Copacabana (Rio de Janeiro) und in Belém (Lissabon).
1. Symmetriearten
- Die Art der Symmetrie, die Achsensymmetrie genannt wird, wird mit einem Stern * gekennzeichnet. Ein gewöhnlicher Stuhl zeichnet sich beispielsweise nur durch Ebenensymmetrie aufgrund einer (Mittel-)Ebene aus; infolgedessen wird für ihn die Symmetriebezeichnung * verwendet. Wenn sich mehrere Spiegel(-achsen) wie in einem Kaleidoskop schneiden, gibt man auch ihre Anzahl in jedem Schnittpunkt an. Die Pflasterung mit Netzmuster beispielsweise, die in Abbildung 2 gezeigt wird, wird – wie Karopapier – durch verschiedene Achsenspiegelungen erzeugt. Hierin konzentrieren wir uns nun auf einen dreieckigen Bereich, der von drei Spiegelachsen begrenzt wird (ein Achtel eines Vierecks), was als Fundamentalbereich bezeichnet wird. Wenn wir uns vorstellen, in diesem Dreieck zu stehen, umgeben von den drei Spiegeln, so könnten wir das gesamte Gehwegpflaster sehen, das sich bis ins Unendliche wiederholt. Nachdem wir darauf abzielen, diese Symmetrien zu charakterisieren, müssen wir die Winkel dieser Dreiecke bestimmen oder aber alternativ die Anzahl der Spiegelachsen, die sich an jeder Ecke schneiden: Es schneiden sich vier Spiegelachsen in der Mitte eines Vierecks, vier in jeder Ecke und zwei in der Mitte einer jeden Teilstrecke, weshalb die Bezeichnung * 4 4 2 lautet.
- Eine Drehsymmetrie, die keine Achsensymmetrie ist, wird durch den (kleinsten positiven) Drehwinkel gekennzeichnet, welcher ein Bruchteil von 360 Grad ist. Das Muster in Abbildung 3 etwa wird durch Drehungen erzeugt. All seine Drehzentren entsprechen einem der drei verschiedenen Punkte in der Abbildung, deren Winkel 360°/4, 360°/4 und 360°/2 sind. Die dazugehörige Bezeichnung setzt sich aus den Nennern der Brüche zusammen: 4 4 2.
- Die Gleitspiegelungssymmetrie wird durch ein Kreuz, X, symbolisiert, und tritt auf, wenn eine Achsenspiegelung mit einer Verschiebung (längs der Spiegelachse) kombiniert wird.

Abbildung 4: Pflasterung in vier Farben nahe dem Hieronymuskloster in Lissabon mit der Bezeichnung X X.
- Einem Muster, das keine der vorhergehenden Symmetriearten aufweist, wird als Verschiebungssymmetrie bezeichnet, wenn das Muster nach einer Verschiebung mit sich selbst zur Deckung kommt, gekennzeichnet mit
 . Für den „Gehweg“ beispielsweise, den man in Abbildung 5 sehen kann, wurde der Pflasterung des Platzes der Restauratoren ein Muster entnommen und sowohl horizontal als auch vertikal wiederholt.
. Für den „Gehweg“ beispielsweise, den man in Abbildung 5 sehen kann, wurde der Pflasterung des Platzes der Restauratoren ein Muster entnommen und sowohl horizontal als auch vertikal wiederholt.
2. Muster in der Ebene
Eine Metapher kann helfen, die 17 Muster bezüglich der Bezeichnung herauszufinden. Angenommen das Restaurant „Symmetrie“ bietet die folgende Speisekarte an:
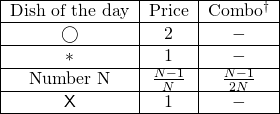
| † Die Zahlen 2, 3, 4 … ergeben 50% Ermäßigung, sofern diese rechts von einem * angeboten werden. Die 3 kostet beispielsweise 2/3 Euro, die Kombination * 3 jedoch nur 1 + 1/3 = 4/3 Euro. |
Wir stellen uns vor, dass in schwierigen Zeiten lediglich 2 Euro für ein Mittagessen vorgesehen sind. Was können wir dafür bekommen, wenn wir das ganze Budget aufbrauchen? Die Variante * 4 4 2 etwa kostet ![]() Euro, ebenso wie die Variante
Euro, ebenso wie die Variante ![]() mit
mit ![]() Euro.
Euro.
Satz für Ebenen: Die Klassen der Muster in der Ebene sind äquivalent zu den Kombinationen von Symbolen, deren Gesamtkosten sich genau auf 2 belaufen.
Was sind die Klassen von Mustern und woher kommt dieser Satz?
Wenn man diesen Lehrsatz anwendet, so ist die Antwort auf die erste Frage nicht mehr als eine Übung. Man sollte anmerken, dass bei Nichtvorhandensein eines Sterns jede Ziffer mindestens ein Halb kostet und immer weniger als 1 ist. Folglich lautet die erste Liste von Bezeichnungen ohne Stern:
6 3 2, 4 4 2, 3 3 3, 2 2 2 2, X X, 2 2 X, O.
Seien a, b, c Zahlen, dann belaufen sich die Kosten der Kombination * a b c auf 2, wenn a b … c gerade 2 kostet. Demzufolge stellt die vorhergehende Liste die Quelle der damit verbundenen Liste von Bezeichnungen dar, die mit * beginnt:
* 6 3 2, * 4 4 2, * 3 3 3, * 2 2 2 2, * X, * *.
Wenn man Brüche hinzunimmt, erhält man die Liste mit gemischten Bezeichnungen:
4 * 2, 3 * 3, 2 * 2 2, 2 2 *.
Auf diese Weise kann man erkennen, dass es höchstens 17 Klassen von diesen Mustern gibt.
Für die zweite Frage empfiehlt es sich, den Text [NOS] heranzuziehen, um die Herkunft des Satzes herauszufinden. Das Buch [CBG] enthält eine ausführlichere Darstellung und faszinierende Abbildungen. Es erklärt auch, in welchen Räumen die Muster liegen, deren Kosten ungleich 2 sind.
3. Mathematik der Kopfsteinpflaster
Portugiesische Kopfsteinpflaster wurden im 19. Jh. als eine Methode erdacht, um Gefangene im Castello São Jorge zu beschäftigen. Seitdem erlangten sie Kultstatus für die Stadt Lissabon und es ist genau dieser Pflasterstil, der vor allem für Plätze in den historischen Bereichen Portugals verwendet wird.
Das bekannteste Muster ondas do mar largo (frei übersetzt mit „Wellen der offenen See“) wurde 1849 für den Praça de Dom Pedro IV, gemeinhin bekannt als Rossio, eingesetzt und 1906 mit großem Erfolg an die Copacabana exportiert. Siehe Abbildung 1. Merkwürdigerweise war König Peter IV von Portugal als Peter I der erste Kaiser von Brasilien.
In ondas do mar largo kann man (viele) äquivalente Spiegelachsen erkennen und auch zwei Typen (schwarz und weiß) von Drehung, um die Punkte, an denen der Abstand zwischen den Wellen am kleinsten ist. Daher ist die Bezeichnung 2 2 *. Siehe Abbildung 6.
Kann man alle Klassen von Symmetrie in portugiesischen Kopfsteinpflastern finden?
In Lissabon wurde eine Studie ins Leben gerufen, die alle Symmetrieklassen, die in portugiesischen Kopfsteinpflastern aufzufinden sind, untersucht und eine Vervollständigung der Liste anstrebt. Der Typ 4 * 2 wurde in Guimarães entdeckt. Und die folgenden Bezeichnungen konnten noch nicht ausfindig gemacht werden:
![]()
Während der Typ ![]() in Abbildung 5 veranschaulicht wird, so sind die vier Typen, die noch zu identifizieren sind, in den Einzelheiten der Muster von Abbildung 7 zu finden. Mehr Beispiele findet man bei [PEF].
in Abbildung 5 veranschaulicht wird, so sind die vier Typen, die noch zu identifizieren sind, in den Einzelheiten der Muster von Abbildung 7 zu finden. Mehr Beispiele findet man bei [PEF].

Abbildung 7: Ausschnitt eines Korbs, einer Tischplatte, eines Kaleidoskopbilds und eines Schwamms, die jeweils die Symmetrieklassen 6 3 2, 3 3 3, * 3 3 3, 2 2 X veranschaulichen.
Wir bestärken unsere Leser, solche Muster als Pflasterungen in ihrer eignen näheren Umgebung zu suchen. Die Autorin dankt allen Beiträgen per E-Mail aus aller Welt!
4. Literaturnachweis
[CBG] Conway, J. H., H. Burgiel, C. Goodman-Strauss, The Symmetries of Things, A K Peters, 2008.
[NOS] Cannas da Silva, A., Um Novo Olhar Sobre Simetria, http://www.math.ethz.ch/~acannas/Outreach.
[PEF] Padroes em Falta, http://www.math.ethz.ch/~acannas/Outreach.
[SPP] Simetria Passo a Passo – Matematica nas Calcadas de Lisboa, http://www.math.ist.utl.pt/simetria.
[WPG] Wallpaper Group, http://en.wikipedia.org/wiki/Wallpaper group.
Institut für Mathematik, ETH Zürich, 8092 Zürich, Schweiz, und Institut für Mathematik, Instituto Superior Tecnico, 1049-001 Lissabon, Portugal
Die Arbeit wurde teilweise von der Stiftung für Wissenschaft und Technologie (FCT Portugal) und von der Stiftung Gulbenkian (Portugal) unterstützt; Fotos von Lissabon von Joao Ferrand; Fotos in Abbildung 7 von Dror Bar-Natan.
| Verbesserung ( von Marston Conder, Universität Auckland): Die erste Person, die diese Erklärung entdeckte, war weder Thurston noch Conway, sondern Murray Macbeath (A.M. Macbeath) einige 20 Jahre früher mit seiner Arbeit über kristallographische Gruppen (in einem größeren Zusammenhang). Seine Beobachtungen wurden wiederentdeckt von einer Reihe von Leuten einschließlich Thurston, aber Macbeath verdient die Anerkennung für die Erklärung, die teilweise algebraischer Natur war. Conway veröffentlichte es und entwickelte eine neue Notation dafür. |




