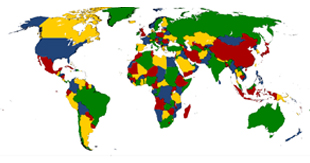
This picture is a property of mathscareers.org.uk, who kindly granted permission to use it in this work.
Originating author is Marcelo Escudeiro Hernandes.
By the famous “Four Colour Theorem”, only four colours we need to colour a map so that no bordering regions have the same colour. Using polynomial equations and Gröbner bases we can determine if three colours are sufficient for a particular map.
1. Map Colouring
The celebrated Four Colours Theorem (1) states that all maps, whether in a plane or sphere, can be coloured with four colours without neighbouring regions being the same colour. It is very easy to produce examples of maps that cannot be coloured with three colours and others that can. A way to decide if three colours are sufficient to colour one particular map, is to analyse a polynomial system associated to the map. Each colour is represented by a complex cubic root of the unit and each region by a variable ![]() such that it can assume only one of three values, that is, one of the three colours. Thus, we have
such that it can assume only one of three values, that is, one of the three colours. Thus, we have ![]() for each region.
for each region.
For regions ![]() and
and ![]() , we have
, we have ![]() . If
. If ![]() and
and ![]() are neighbouring regions, and as neighbouring regions cannot have the same colour, then
are neighbouring regions, and as neighbouring regions cannot have the same colour, then ![]() , that is,
, that is, ![]() . In this way, a map with
. In this way, a map with ![]() regions can be colored with three colours if, and only if, the system of polynomial equations
regions can be colored with three colours if, and only if, the system of polynomial equations
(1) ![]()
where ![]() and
and ![]() and
and ![]() represent adjacent regions, has at least one solution.
represent adjacent regions, has at least one solution.
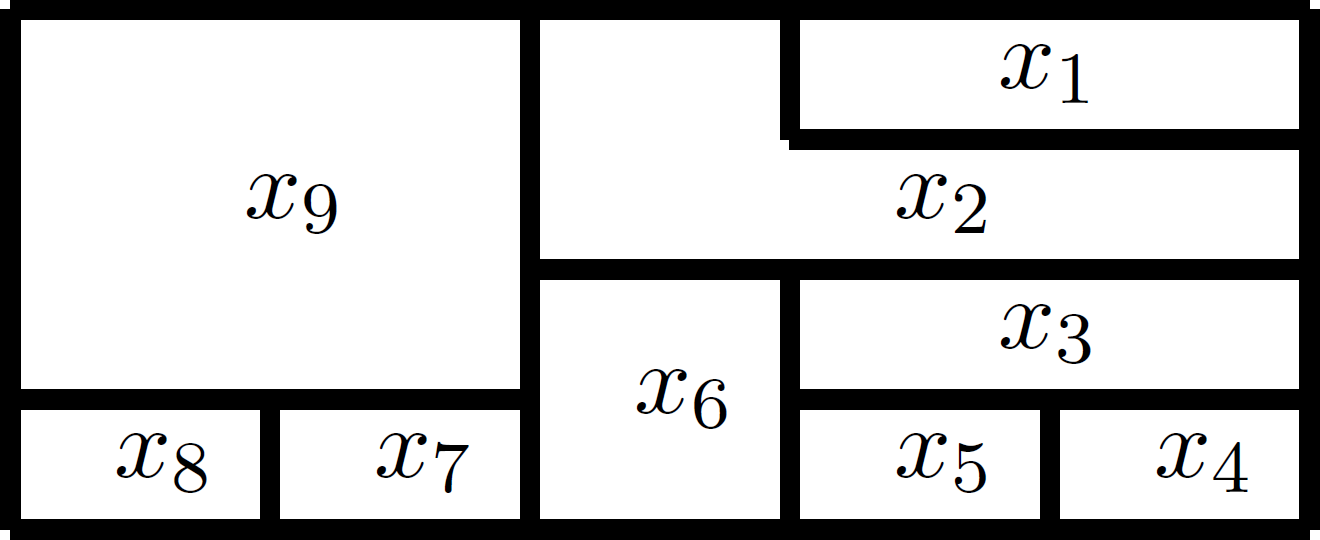
Example 1.
We consider the map:
Can it be colored with three colours?
To answer this question we must verify that the polynomial system 1 with ![]() and
and
![]()
can be solved.
2. Systems of polynomial equations
The answer of many problems in mathematics is due to the solution of systems of polynomial equations, which is not always easy. If the system is given by linear equations, we can, through Gaussian elimination, substitute the system for another equivalent whose solution is simpler. In the case of polynomial systems, it has an analogous method that we describe below.
We will denote by ![]() the set of polynomials with complex coefficients with variables
the set of polynomials with complex coefficients with variables ![]() . Given a set of polynomials
. Given a set of polynomials ![]() in
in ![]() , we determine the ideal generated for them as being
, we determine the ideal generated for them as being
![]()
A theorem due to the mathematician David Hilbert <http://www.mat.uniroma1.it/people/manetti/dispense/nullstellen.pdf”>(2), called Hilbert’s Nullstellensatz, states that the system ![]() admits a (complex) solution if and only if
admits a (complex) solution if and only if ![]() . But how can we check the last condition?
. But how can we check the last condition?
It is very simple to verify that two systems of equations ![]() and
and ![]() , where
, where ![]() , satisfying the condition
, satisfying the condition
(2) ![]()
have the same solution.
Therefore, the strategy to solve a system ![]() consists to find polynomials
consists to find polynomials ![]() which satisfy the condition 2 and with which it is possible to test if a given
which satisfy the condition 2 and with which it is possible to test if a given ![]() belongs or not to the ideal
belongs or not to the ideal ![]() and whose common solution is easier to compute than the original system.
and whose common solution is easier to compute than the original system.
The existence of such ![]() was discovered theoretically during the first half of the last century by the mathematician Wolfgang Gröbner. Some years later, his student Bruno Buchberger created an algorithm to compute it. These sets are called Gröbner bases and Buchberger’s algorithm to compute them is one of the most important tools of algebraic computation.
was discovered theoretically during the first half of the last century by the mathematician Wolfgang Gröbner. Some years later, his student Bruno Buchberger created an algorithm to compute it. These sets are called Gröbner bases and Buchberger’s algorithm to compute them is one of the most important tools of algebraic computation.
If the ideal is of the form ![]() , we have
, we have ![]() if and only if
if and only if ![]() , that is,
, that is, ![]() is divisible by
is divisible by ![]() . Analogously,
. Analogously, ![]() if and only if
if and only if ![]() , which suggests something similar for the division of
, which suggests something similar for the division of ![]() by
by ![]() . In fact, we can divide a polynomial in several variables by a finite set of polynomials, provided that the monomials are ordered in some way.
. In fact, we can divide a polynomial in several variables by a finite set of polynomials, provided that the monomials are ordered in some way.
3. Gröbner Bases
A monomial ![]() of
of ![]() is an element of the form
is an element of the form ![]() , where
, where ![]() non-negative integers. The monomial
non-negative integers. The monomial ![]() will be denoted by
will be denoted by ![]() . Among the orders
. Among the orders ![]() on the monomials of
on the monomials of ![]() , the ones that satisfy
, the ones that satisfy ![]() and
and ![]() whenever
whenever ![]() are the ones which make it possible to put into practice the algorithm of the division.
are the ones which make it possible to put into practice the algorithm of the division.
An example is the lexicographical order ![]() , where
, where ![]() , if there exists
, if there exists ![]() such that
such that ![]() and
and ![]() for all
for all ![]() .
.
Fixed an order on the monomials, the greatest monomial of a polynomial ![]() it is called the leading term of
it is called the leading term of ![]() and denoted by
and denoted by ![]() .
.
A Gröbner basis of an ideal ![]() with respect to a given monomial order, is, by definition, any set
with respect to a given monomial order, is, by definition, any set ![]() of elements of
of elements of ![]() such that the leading term of any element of
such that the leading term of any element of ![]() is divisible by the leading term of some element of
is divisible by the leading term of some element of ![]() . We can show that any Gröbner basis
. We can show that any Gröbner basis ![]() of
of ![]() is a set that satisfies the condition 2.
is a set that satisfies the condition 2.
Therefore, ![]() if and only if there exists a Gröbner basis of
if and only if there exists a Gröbner basis of ![]() containing a non-zero constant, since
containing a non-zero constant, since ![]() , for all monomial
, for all monomial ![]() of
of ![]() .
.
For example, ![]() is a Gröbner basis of
is a Gröbner basis of ![]() , with respect to any monomial order, whereas
, with respect to any monomial order, whereas ![]() is not a Gröbner basis of
is not a Gröbner basis of ![]() with respect to the lexicographical order, because
with respect to the lexicographical order, because ![]() is not divisible by
is not divisible by ![]() .
.
To get a Gröbner basis of an ideal, with respect to a chosen monomial order, you can apply Buchberger’s algorithm (3). We find algorithms to calculate Gröbner bases in a majority of computer algebra systems.
For instance, a Gröbner basis for the ideal ![]() , with respect to the lexicographical order is
, with respect to the lexicographical order is ![]() .
.
4. Solution of the problem and other applications
The system given in Example 1, has at most a finite number of solutions (nine variables, each of them being able to take one of three values). The problem is to determine if the system admits any solution, and in that case, to determine it.
Applying Buchberger’s algorithm to the system of Example 1, we get the following Gröbner basis ![]() , with respect to the lexicographical order:
, with respect to the lexicographical order:
![]()
Therefore, ![]() and,consequently, the system admits solutions. The equations
and,consequently, the system admits solutions. The equations
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} x_1 ^3 - 1 = 0 ~,\\ x_2 ^2 + x_2 x_1 + x_1 ^2 = 0 ~,\\ x_5 - x_2 = 0 ~,\\ x_7 - x_2 = 0 ~,\\ x_9 -x_3 = 0 ~, \end{array}\right.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-eee384611a0c9f1bf1e2e038dc6a0a94_l3.png)
translate the following fact: we can use any colour for ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
As the colours are represented by the complex cubical roots of the unit, the only solution for ![]() ,
, ![]() and
and ![]() is to attribute values (colours) distinct for
is to attribute values (colours) distinct for ![]() ,
, ![]() and
and ![]() , and thus,
, and thus, ![]() . Finally,
. Finally, ![]() gives us two
gives us two
possibilities: ![]() or
or ![]() , that is,
, that is, ![]() ,
, ![]() and
and ![]() take distinct colours or
take distinct colours or ![]() . And thus, we find, up to permutations of the colours, all the possible solutions:
. And thus, we find, up to permutations of the colours, all the possible solutions:
Gröbner bases also can be used to operate with ideals, converting parametric equations to their implicit equations (some surfaces and curves for examples) into nonparametric equations, to compute the minimum polynomial of algebraic numbers, to verify theorems of Euclidean Geometry, to validate constructions with Origami and to solve Sudoku puzzles (See (4), (5) and (6)).
References
(1) http://www.ipv.pt/millenium/Millenium24/12.pdf
(2) http://www.mat.uniroma1.it/people/manetti/dispense/nullstellen.pdf
(3) https://www.risc.jku.at/people/buchberg/papers/1970-00-00-A.english.pdf
(4) Adams, W. and Loustaunau, P., An Introduction to Gröbner Basis, AMS, Providence RI (1994).
(5) Cox, D; Little, J. and O’Shea, D., Ideals, Varieties and Algorithms, 2nd edition, Springer-Verlag, New York, (1996).
(6) Hernandes, M. E., Um Primeiro Contato com Bases de Gröbner, 28°. Colóquio Brasileiro de Matemática, IMPA, Rio de Janeiro, (2011).


Are ordinary senior secondary teachers supposed to be able to understand this?
This article is not in keeping with the Klein blog. It’s way way too difficult to follow along. I was excited about the complex numbers connection but I’d need to be a trained university lecturer to make sense of this…
It is not that hard… You only need to have some knowledge in ideals and rings to understand it, and these notions are taught in 3rd year of university. Some vignettes require a little effort !
I think for secondary teachers to struggle with an article like this. It helps them get some insights into the world beyond “precalc”, etc.
Would be useful to have an accompanying reference on “Groebner for Beginners” to help with some examples.
Michael Trott, at Wolfram Research, wrote some interesting articles on solving problems with Groebner bases. Mathematica is more universal now than it used to be, and these might also be helpful.