
 Originating author is Christiane Rousseau.
Originating author is Christiane Rousseau.
How do we measure the size of a geometric object? For subsets of the plane we often use perimeter, length, area, diameter, etc. These are not sufficient to describe fractals. The fractal objects are very complex geometric objects, and we must find a way to quantify their complexity. For this purpose the mathematicians have introduced the concept of dimension. Dimension provides a measure of the complexity of a fractal. The notion of dimension is a generalization and formalization of our intuitive notion of dimension when we speak of 1D, 2D or 3D. We will discuss some ways to describe fractal objects by working on two examples: the Sierpinski carpet and the von Koch flake (see figures on the left).
What is the area of the Sierpinski carpet?
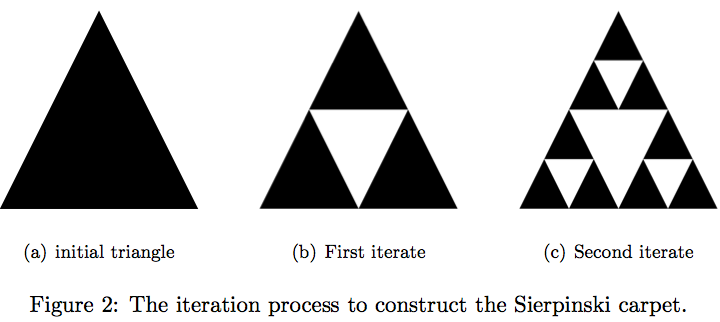
We first need to understand the construction of the Sierpinski carpet (see Figure 2). It is done through an iterative process. We start with a triangle and, at each step, we remove the middle triangle. We are left with three triangles. Within each remaining triangle we remove the middle triangle, etc.
We now have all the ingredients to compute the area of the Sierpinski carpet. Let us suppose that the area of the initial triangle (see Figure 2(a)) is ![]() .
.
- At the first iteration we remove an area of
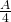 and we are left with an area of
and we are left with an area of 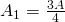 .
.
- At the second iteration, we remove one fourth of the area of the three remaining triangles, so one fourth of
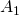 . Hence, the remaining area is
. Hence, the remaining area is 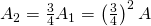 .
.
- At the third iteration, we remove one fourth of the area of the nine remaining triangles, so one fourth of
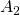 . Hence, the remaining area is
. Hence, the remaining area is 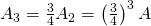 .
.
- …
- At the
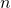 -th iteration we remove one fourth of the area of the
-th iteration we remove one fourth of the area of the 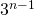 remaining triangles, so one fourth of
remaining triangles, so one fourth of 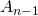 . Hence, the remaining area is
. Hence, the remaining area is 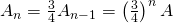 .
.
- …
Since
![]()
we can conclude that the area of the Sierpinski carpet is zero!
What is the length of the von Koch flake?
Again, the von Koch flake is obtained by iteration. At each step of the iteration, we replace each segment by a group of 4 segments, each segment with length equal to ![]() of the length of the original segment (see Figure 3). If
of the length of the original segment (see Figure 3). If ![]() is the length of the original triangle in Figure 3(a), then
is the length of the original triangle in Figure 3(a), then ![]() is the length of the star of Figure 3(b),
is the length of the star of Figure 3(b), ![]() is the length of the object in Figure 3(c), etc. In particular, this means that, at each step, the length is multiplied by
is the length of the object in Figure 3(c), etc. In particular, this means that, at each step, the length is multiplied by ![]() . Since there are an infinite number of steps in the construction, then the length of the von Kock flake is infinite!
. Since there are an infinite number of steps in the construction, then the length of the von Kock flake is infinite!
The Sierpinski carpet is a very complicated object. Nevertheless, its area is zero and hence, gives us little information on the object. The fact that the length of the von Koch flake is infinite tells us that the object is complicated, but no more precision. To be able to give more information on fractal objects the mathematicians introduce the concept of dimension.
We start with our intuitive idea of dimension. Intuitively, smooth curves are of dimension ![]() , smooth surfaces of dimension
, smooth surfaces of dimension ![]() , and filled volumes of dimension
, and filled volumes of dimension ![]() . So we should give a mathematical definition of dimension which yields
. So we should give a mathematical definition of dimension which yields ![]() for smooth curves,
for smooth curves, ![]() for smooth surfaces, and
for smooth surfaces, and ![]() for filled volumes. In the context of this vignette we will limit ourselves to dimensions
for filled volumes. In the context of this vignette we will limit ourselves to dimensions ![]() and
and ![]() . We want to cover a geometric object in the plane with small squares. (If we would want to define dimension
. We want to cover a geometric object in the plane with small squares. (If we would want to define dimension ![]() we would use small cubes, but we could have used small cubes for curves and surfaces without changing the dimension!)
we would use small cubes, but we could have used small cubes for curves and surfaces without changing the dimension!)
Case of a smooth curve. (see Figure 4)
- if we take squares with side of half size, then we need approximately twice as much squares to cover the object;
- if we take squares with side one third of the size, then we need approximately three times as much squares to cover the object;
- …
- if we take squares with side
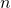 times smaller, then we need approximately
times smaller, then we need approximately 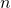 times more squares to cover the object;
times more squares to cover the object;
Case of a surface. (see Figure 5)
- if we take squares with side of half size, then we need approximately four times more squares to cover the object;
- if we take squares with side one third of the size, then we need approximately nine times more squares to cover the object;
- …
- if we take squares with side
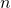 times smaller, then we need approximately
times smaller, then we need approximately 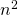 times more squares to cover the object;
times more squares to cover the object;

We can now give the (intuitive) definition of dimension:
Definition. An object in the plane has dimension ![]() if, when we take squares with edge
if, when we take squares with edge ![]() times smaller to cover it, then we need approximately
times smaller to cover it, then we need approximately ![]() more squares to cover it.
more squares to cover it.
Some remarks on our definition.
- Of course the squares utilized to cover the object could have been slanted. Also they could overlap.
- Instead of squares we could have used only rectangles of the same sizes with a ratio
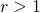 of the length by the width. We would have get the same results for dimension
of the length by the width. We would have get the same results for dimension  and
and 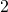 and this is also the case for the general case of dimension
and this is also the case for the general case of dimension 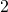 . To calculate the dimension of the von Koch flake it is easier to use rectangles than squares.
. To calculate the dimension of the von Koch flake it is easier to use rectangles than squares.
The definition can be generalized to geometric objects which are subsets of ![]() and the result is independent of the
and the result is independent of the ![]() we consider!
we consider!
Definition. A subset of ![]() has dimension
has dimension ![]() if, when we take
if, when we take ![]() -dimensional hypercubes with edge
-dimensional hypercubes with edge ![]() times smaller to cover it, then we need approximately
times smaller to cover it, then we need approximately ![]() more hypercubes to cover it.
more hypercubes to cover it.
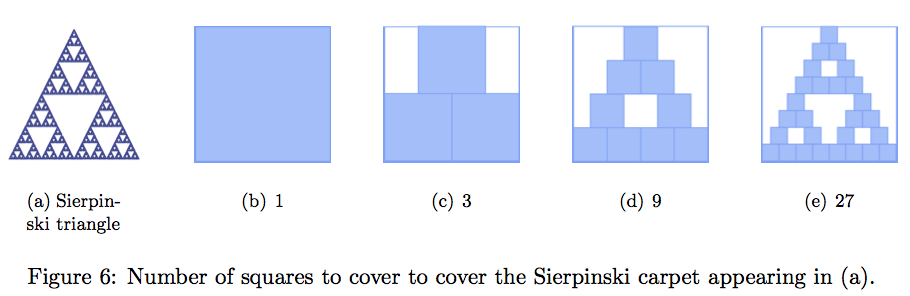
Not all objects have a dimension. But, the self similar objects have a dimension which, most often, is not an integer. Let us now calculate the dimension of the Sierpinski carpet (see Figure 6).
- Let us take a square with side equal to the length of the base. It covers the Sierpinski carpet of Figure ?(a).
- if we take squares with side of half size, then we need three squares to cover it. Note that
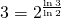 (Figure ?(c)).
(Figure ?(c)).
- if we take squares with side one fourth of the size, then we need nine squares to cover it. Note that
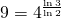 (Figure ?(d)).
(Figure ?(d)).
- if we take squares with side one eight of the size, then we need
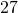 squares to cover it. Note that
squares to cover it. Note that 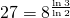 (Figure ?(e)).
(Figure ?(e)).
So, it is easy to conclude that the dimension of the Sierpinski triangle of Figure ?(a) is ![]() .
.
We now assert that the dimension of the von Koch flake of Figure ?(b) is ![]() . Why? If we try to cover it with squares with side having the length of one side of an iterate as in Figure ?, one difficulty comes from the fact that some squares cover one side, and some can cover two sides when these sides form a peak. So let us use the trick of our second remark and use rectangles with length
. Why? If we try to cover it with squares with side having the length of one side of an iterate as in Figure ?, one difficulty comes from the fact that some squares cover one side, and some can cover two sides when these sides form a peak. So let us use the trick of our second remark and use rectangles with length ![]() times the width. We give the main steps of the argument, and we let you fill in the details. At each iterate, we use as many rectangles as sides of the iterate, with the length of the rectangle equal to the length of the side of the iterate. If we place the rectangles on the outer side of the von Koch flake, then they will cover the new peaks that will be added at the next iterates. It is easy to check that we need as many rectangles as sides. In the initial triangle we had three sides and, from one iterate to the next, we multiply the number of sides by
times the width. We give the main steps of the argument, and we let you fill in the details. At each iterate, we use as many rectangles as sides of the iterate, with the length of the rectangle equal to the length of the side of the iterate. If we place the rectangles on the outer side of the von Koch flake, then they will cover the new peaks that will be added at the next iterates. It is easy to check that we need as many rectangles as sides. In the initial triangle we had three sides and, from one iterate to the next, we multiply the number of sides by ![]() , so we multiply the number of rectangles by
, so we multiply the number of rectangles by ![]() . At the same time we use rectangles with sides
. At the same time we use rectangles with sides ![]() times as small. Since
times as small. Since ![]() , we conclude that the dimension of the von Koch flake is
, we conclude that the dimension of the von Koch flake is ![]() .
.
The dimension gives a “measure” \ of the complexity or density of a fractal. Indeed, we feel that the Sierpinski carpet is denser than the Von Koch flake, which looks more like a thickened curve. This is reflected by the fact that ![]() .
.
Applications
The capillary network in the neighborhood of a tumor. it is not the same as elsewhere in the body. Research is carried on this, and in particular on its fractal dimension, in order to improve diagnosis from medical imaging.
The design of the bronchial tree. High level athletes are more likely to suffer from asthma than the general population. Why? The paper [Ma] studied the “optimal” lung. There are 17 level of bronchial tubes before arriving to the terminal bronchioles followed by the acini involved in air exchange. If the bronchial tubes are too thin, then the pressure increases when the air penetrates in the next level of bronchial tubes. But it they are too wide, so that the volume remains the same at each level, then the volume becomes too large. (It would become infinite if we had an infinite number of levels). So, the “optimal” lung would have the minimum volume without increasing the pressure. But, near the optimal lung, a small decrease in the diameter of bronchial tubes leads to a much higher increase of pressure than the same decrease in wider bronchial tubes. (This comes from the special nonlinear form of the function giving the pressure.) The human lungs have wider bronchial tubes and a higher volume than the theoretical optimal lung. This buffer provides a protection in case of bronchoconstriction, a pathology decreasing the diameter of the bronchial tubes, which could be caused by asthma. Athletes have lungs generally closer to the theoretical optimal lung, and hence are more vulnerable.
The small intestine. The outer surface of the small intestine has an approximate area of ![]() , while the inner surface has an approximate area of
, while the inner surface has an approximate area of ![]() . We have seen with the von Koch flake that a fractal curve can have an infinite length, even if it lies in a finite surface. Similarly, we could easily imagine that a fractal surface lying in a finite volume can have an infinite area. This is a trick used by nature: the area of the inner surface of the small intestine must be very large in order to maximize intestinal absorption. The fractal nature of this surface achieves this goal. The same is true for the surface of the alveoli at the end of the bronchioles in the lungs. Since the bronchial tree has a fractal nature, the surface of the alveoli is extremely large, thus maximizing the gas exchange.
. We have seen with the von Koch flake that a fractal curve can have an infinite length, even if it lies in a finite surface. Similarly, we could easily imagine that a fractal surface lying in a finite volume can have an infinite area. This is a trick used by nature: the area of the inner surface of the small intestine must be very large in order to maximize intestinal absorption. The fractal nature of this surface achieves this goal. The same is true for the surface of the alveoli at the end of the bronchioles in the lungs. Since the bronchial tree has a fractal nature, the surface of the alveoli is extremely large, thus maximizing the gas exchange.
Bibliography
[Ma] B. Mauroy, M. Filoche, E.R. Weibel, B. ~Sapoval, An optimal bronchial tree may be dangerous, Nature, 427 (2004), 633–636.
Originating author is Christiane Rousseau.



Pingback: Classifying objects | Klein Project Blog